線形計画法

数理モデルへの定式化演習

　

以下の問題を数理モデルに定式化し，ＬＩＮＤＯを利用して最適な解を求めよ.

　

注意：

  1. （決定）変数に何を取るか, 制約条件は何か良く考えること.
  2. ＬＩＮＤＯに定式化した問題を入力する時は，変数の名前をわかりやすいように工夫した方が良い.
    3. 問題にある数値がそのままモデルの中の係数（数字）になるとは限らない.数値データの単位の統一に気を付けよう．

　

問題1

文教工業には，３台の機械Ｍ１，Ｍ２，Ｍ３がある．これらを用いて加工できる製品は６種類あって，それぞれ１個当たりの各機械の処理時間および利益は以下の表のとおりである. また，各機械の１日の使用時間は１０時間である．利益が最大になるような生産計画を立てよ.

　

問題２

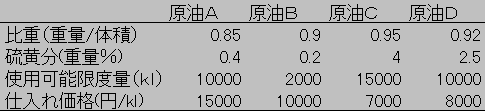
下表の４種類の原油を混合してできるだけ原料費が安く, しかも硫黄分が１％以下の重油を10000キロリットル生産したい. 各原油の最適な混合量を求めよ.

　

問題３

文教米店ではある穀物を仕入れて販売している. 倉庫には100トンまで貯蔵できる. 向こう3ヶ月間（1月,2月,3月）の仕入れ, 販売,月末在庫量を，利益が最大になるように求めたい. 各月の仕入れ価格, 販売価格，在庫費, 需要の最大見込み量は次のように見積もられている．なお，一月の期首在庫は0であり，3月末には30トン以上の在庫を残しておきたい.

　

問題４

飛行中に互いに空中給油可能な，性能の全く同じ飛行機が３機ある(１号機,２号機,３号機)．

３機ある飛行機で協力して３号機だけをなるべく基地から遠くに飛ばしたい．ただし，１号機と２号機は基地に戻らなくてはならない. どのような３機の飛行計画を立てればよいか.

　

問題5

文教製紙では幅540ｃｍ，長さ５０ｍの紙ロールを生産している．

これを用いて幅150ｃｍ，長さ50ｍの紙ロールを10本，幅120ｃｍ，長さ50ｍの紙ロールを20本，幅70ｃｍ，長さ50ｍの紙ロールを30本作りたい.

最小限必要な紙ロールの数は何本くらいか?

注意：