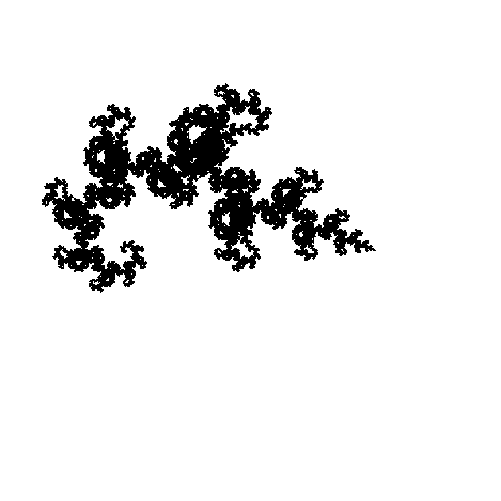『教育研究所紀要第5号』文教大学付属教育研究所1996年発行
自己相似図形を利用する幾何教育の可能性
白石和夫(文教大学教育学部)
要約
JIS Full BASICを利用すると,自己相似図形をその定義に忠実に近似して描くことができる。自己相似図形を動機づけに利用し,Full BASICの絵定義の変換機能を活用すれば,ベクトル・行列と変換幾何を優先する,従来とは異なったアプローチによる幾何教育が可能となる。
キーワード: 自己相似図形,幾何教育,フラクタル,Full BASIC
1.はじめに
米国のNational Concil of Teachers of Mathematics (NCTM,全米数学教師協会) は,"Fractals for the Classroom"という全2冊,総計950ページにおよぶ書物をSpringer-Verlagと共同で発刊した1)。さらに,それぞれに "Strategic Activities"という名称のワークシートが用意されており,それを含めれば,総ページ数はさらに多くなる。この書物自体は,実際の教室で教えることを意図したものではないようであるが,新しい数学に対するNCTMの意気込みを感じることができる。
近年,カオス,フラクタルが大きな関心を集めている。この分野の解説書にはコンピュータグラフィックスによる図形が描かれ,読者を魅了している。放送大学にも「カオスとフラクタル入門」2)という講義が開設され,その講義を担当する山口昌哉氏は,日本数学教育学会の平成7年度全国大会で,「戦後50年の数学は何をもたらし,未来に何を期待されるか」という表題の講演において,カオスとフラクタルを中心に述べている。また,本学教育学部においても,フラクタルを卒業研究に選ぶグループが現れている(平成7年度)。
ここ数年のパーソナルコンピュータの性能の向上は著しいものがあり,従来は書物の中でしか見ることのできなかったこれらの図形が,実際に手元のパソコンでプログラムを動かして描くことができるようになってきた。
本稿では,自己相似図形をとりあげ,自己相似図形を幾何の学習の動機づけとして用いる幾何教育の可能性を探る。まず,ISOにより標準化されたプログラミング言語JIS Full BASIC3)を用いることで,自己相似図形がその定義に忠実に近似できることを示す。そして,学校数学における幾何教育のあり方について考察し,変換幾何の学習を学校数学に取り入れるための方策について考察する。
2.自己相似図形
(1) 一般論
相似縮小変換f 1,f 2 に対して,f 1(D)∪f 2(D) =D
となる図形Dを自己相似図形という4)。
Dは有界であるものと仮定すれば,Dを描く手続きを次のように作成することで,Dを描くことができる。
Dを描く手続き f 1(D)を描く
f 2(D)を描く
手続きの終わり
f 1,f 2が縮小写像であることから,この再帰手続きを繰り返すと,描くべき図形の直径はディスプレーの解像度に比べて十分に小さくなる。そのとき,問題の図形を1点で代替して描くことができる。
(2)表向き相似変換の例
まず,表向き相似変換に関する例として, f 1が 原点を中心とする45°の回転と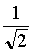 倍の縮小の合成写像, f 2が 点(1,0)を中心とする45°の回転と
倍の縮小の合成写像, f 2が 点(1,0)を中心とする45°の回転と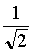 倍の縮小の合成写像である場合を考察する。
倍の縮小の合成写像である場合を考察する。
原点を中心とする角αの回転をrotate(α),原点を中心とするr倍の拡大をscale(r),x軸方向にa,y軸方向にbの平行移動を shift(a , b),変換T1 ,T2の合成をT1 *T2 で表すと, f 1,f 2は,
f 1 = rotate(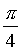 )*scale(
)*scale(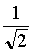 ), f 2 = shift(1,0)*rotate(
), f 2 = shift(1,0)*rotate(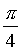 )*scale(
)*scale(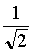 )*shift(1,0)
)*shift(1,0)
と表すことができる。なお,複素数を用いて表せば
f 1( z ) =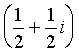 z
z
f 2( z ) =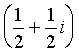
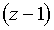 + 1
+ 1
である。
Dを描く手続きのなかでf 1(D)やf 2(D)を描くのに,JIS Full BASICの図形の変換の機能を用いることができる。実際,図形Dを描くプログラムはprogram 1のようになる。
100行から170行までは,図形Dを描くための手続きDを定義する部分である。そして,プログラムの実行は180行から開始される。
180行では,描画領域にx座標の範囲が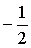 から
から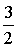 ,y座標の範囲が
,y座標の範囲が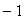 から1までとなる座標系を設定している。描画領域の形状は正方形であるので,x座標の幅とy座標の幅とが等しくなるようにしてある。
から1までとなる座標系を設定している。描画領域の形状は正方形であるので,x座標の幅とy座標の幅とが等しくなるようにしてある。
190行は,120行のplot points文で描かれるマークの形状を・に変更する。
210行は,引数nに0を代入して100行から始まる絵定義(picture)Dを呼び出す文である。100行から始まる絵定義Dで,引数nは再帰の深さを制御するためのものである。140行と150行で再帰的にDを呼び出すときにnを1加算している。nの値が110行のif文で指定している数値18になると再帰呼び出しを終了し,変換された座標系の原点にマークを描く。
140行と150行が,再帰呼び出しを利用してDをf1,f2で変換して描くことによりf 1(D)とf 2(D)を描く部分である。
110行で指定する定数は,おおむね,f1,f2の縮小率sと描画領域の縦横方向のピクセル数pとから決定できる。描くべき図形Dの直径が描画領域の幅より小さいものと仮定すれば,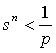 となるようにnを選ぶことが一応の目安になる。
となるようにnを選ぶことが一応の目安になる。
描画領域のピクセル数を501×501として得た実行結果を図1に示す。この図形は,これを並べることによって平面の敷き詰めが可能な図形として知られている。
100 PICTURE D(n)
110 IF n=18 THEN
120 PLOT POINTS: 0,0
130 ELSE
140 DRAW D(n+1) WITH ROTATE(PI/4)*SCALE(1/sqr(2))
150 DRAW D(n+1) WITH SHIFT(-1,0)*ROTATE(PI/4)*SCALE(1/sqr(2))*SHIFT(1,0)
160 END IF
170 END PICTURE
180 SET WINDOW -1/2 , 3/2 , -1 , 1
190 SET POINT STYLE 1
210 DRAW D(0)
220 END |
program 1 |
(3)裏向き相似変換の例
x軸方向にa倍,y軸方向にb倍の拡大をscale(a,b)で表すとき,scale(1,-1)はx軸に関する対称移動を表す。複素数平面では共役数をとる演算に対応する。
f 1( z )=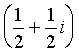 z ,
z ,
f 2( z )=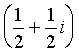
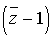 + 1
+ 1
に関する自己相似図形を求めてみると図2のようになる。
プログラムは,150行のWITH以降を
SCALE(1,-1)*SHIFT(-1,0)*ROTATE(PI/4)* SCALE(1/sqr(2))*SHIFT(1,0)
に修正する。
また, f 1( z )=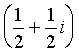 z ,
z ,
f 2( z )=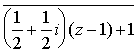
に関する自己相似図形を求めてみると図3のようになる。
プログラムは,150行のWITH以降を
SHIFT(-1,0)*ROTATE(PI/4)* SCALE(1/sqr(2))*SHIFT(1,0)*SCALE(1,-1)に修正したものである。
(4)コッホ曲線
コッホ曲線は,タートルグラフィックスの応用例としてよく知られた図形であるが,それとは別に,自己相似図形の観点から次のように定義することができる。
コッホ曲線は,底辺ABの長さが3で高さが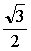 の二等辺三角形CABで,頂点Aを不動点として,点Bを点Cに移し,点Cを線分AB上の点に移すような相似変換をf1,頂点Bを不動点として,点Aを点Cに移し,点Cを線分BA上の点に移すような相似変換をf2とするとき,f 1(D)∪f 2(D)=Dとなる図形Dである。
の二等辺三角形CABで,頂点Aを不動点として,点Bを点Cに移し,点Cを線分AB上の点に移すような相似変換をf1,頂点Bを不動点として,点Aを点Cに移し,点Cを線分BA上の点に移すような相似変換をf2とするとき,f 1(D)∪f 2(D)=Dとなる図形Dである。
ここで,各頂点の座標をA(0,0),B(3,0),C(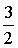 ,
,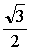 )とし,f1,f2を
)とし,f1,f2を
f1=SCALE(1,-1)*ROTATE(α)*SCALE(r)
f2=SHIFT(-3,0)*SCALE(1,-1)*
ROTATE(-α)*SCALE(r)*SHIFT(3,0)
の形に表すものとすると,縮小写像f1,f2の倍率rは線分ACの長さを線分ABの長さで割って求められ,回転角αは点Cの偏角として求められる。
program 2は,コッホ曲線を描くプログラムである。program 2では,再帰のネスティングの制御にprogram 1とは異なる方法を採用している。200行の絵定義Kochの引数sは総合の縮小率を表す変数である。この値が210行で定める大きさを下回ったとき再帰呼び出しを止める。実行結果を図4に示す。
200 PICTURE Koch(s)
210 IF s<1/500 THEN
220 PLOT POINTS: 0,0
230 ELSE
240 DRAW Koch(s*r) WITH SCALE(1,-1)*ROTATE(alfa)*SCALE(r)
250 DRAW Koch(s*r) WITH SHIFT(-3,0)*SCALE(1,-1)*ROTATE(-alfa)*SCALE(r)*SHIFT(3,0)
260 END IF
270 END PICTURE
280 LET r=SQR((3/2)^2+(SQR(3)/2)^2) / 3
290 LET alfa=ANGLE(3/2,SQR(3)/2)
300 SET WINDOW 0,3,0,3
310 SET POINT STYLE 1
320 DRAW Koch(1)
330 END |
program 2 |
(5)一般の自己相似図形
program 2で用いた手法を応用すれば,f1,f2で縮小率が異なる場合でも効率よく自己相似図形を求めることができる。そして,さらにこの手法は,任意の相似縮小変換f1 ,f2…fkに対して,それらに関する自己相似図形を求めるのに応用することができる。たとえば,シルピンスキーのガスケット(図5)は正3角形の3頂点を中心とする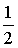 倍の縮小写像に関する自己相似図形である。
倍の縮小写像に関する自己相似図形である。
本稿で述べた手法は再帰を基本とする手法であるが,これを繰り返しのアルゴリズムに転換することができる。その結果得られるアルゴリズムは,Iterated Function System (IFS) 5)として知られるアルゴリズムと一致する。
3 新しい幾何教育の可能性
(1)幾何教育の位置づけ
物理空間に存在する図形そのものを対象とする学問としての幾何学は,理工系の諸科学にとって不可欠の道具である。一方,近年,数学の応用が拡大している人文社会科学系にとって,ユークリッド式の距離の入った空間に関する考察は,ほとんど用をなさない。しかし,多くの生徒にとって,幾何は,コンピュータ・グラフィックスなどを通じて親しみやすい素材となる可能性を持っている。微積分が人文社会科学系に不可欠な道具になりつつある現状も合わせ考えると,幾何は,高等学校における選択数学の中核をなす教材とするのにふさわしいものだと思われる。なお,幾何学には,トポロジーに代表されるように数学的構造の学としての側面があるが,ここでいう幾何は,物理空間の模型としてのユークリッド空間を対象とする幾何のことである。
(2)コンピュータを利用する幾何の学習
現在,高等学校の幾何教育では,図形を方程式で表すことを基礎にした展開がなされている。しかし,幾何を学ぶための道筋は一通りではない。ベクトルや行列を利用して運動を表現する幾何を先に学ぶという行き方も考えられてよいはずである。それは,コンピュータを道具として利用すれば実行可能なことであり,また,逆に,コンピュータを利用する際の応用の観点から有用性が認められる内容である。JIS Full BASICには,次に示す変換が組込まれている。 SHIFT(a,b) 平行移動 ROTATE(α) 原点を中心とする回転移動 SCALE(a,b) 原点を中心とする拡大・縮小 SHEAR(α) 剪断(x,y)→(x + y tanα,y)
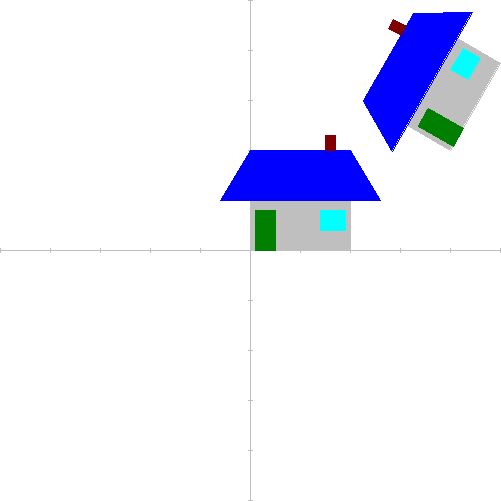
これらの合成により,任意の点のまわりの回転,任意の直線に関する対称移動などが実現できる。実際にプログラムをかいて実行してみることで,これらのことを具体例を通して学習することができる。これらの変換の用い方の一例をprogram 3に,その実行結果を図6に示す。この例はTrue BASIC6)付属のサンプルをヒントにして作成したものである。なお,外部絵定義axesの定義部は省略してある。
(3)変換幾何の教程
変換幾何に関する日本語の書物に,「変換幾何入門」7)がある。コンピュータを利用してこの書に述べられている幾何を実行してみることが可能である。しかし,この書は初等幾何的なアプローチを採用しているために線形代数に慣れた学習者には読みづらい。コンピュータを道具として学ぶ観点では,行列を前面に出したもののほうが扱いやすいし,実用的でもある。行列を前面に出した変換幾何の書としては,Mortensonによるものが出版されている8)。
100 PICTURE House
110 SET AREA COLOR 15
120 PLOT AREA: 0,1; 0,0; 2,0; 2,1 ! 壁
130 SET AREA COLOR 2
140 PLOT AREA: -0.6,1; 2.6,1; 2,2; 0,2 ! 屋根
150 SET AREA COLOR 10
160 PLOT AREA: 0.1,0; 0.1,0.8; 0.5,0.8; 0.5,0 ! ドア
170 SET AREA COLOR 5
180 PLOT AREA: 1.4,0.4; 1.9,0.4; 1.9,0.8; 1.4,0.8 ! 窓
190 SET AREA COLOR 12
200 PLOT AREA: 1.7,2; 1.7,2.3; 1.5,2.3; 1.5,2 ! 煙突
210 END PICTURE
220 SET WINDOW -5,5,-5,5
230 DECLARE EXTERNAL PICTURE axes
240 DRAW axes
250 DRAW House
260 DRAW House WITH ROTATE(PI/3)*SHIFT(4,2)
270 END |
program 3 |
4 終わりに
本稿に述べたプログラムを実行するのに利用可能なBASIC処理系(MS-Windows版とPC9801DOS版)を作成し,インターネットを介して配布している。URLは,http://pweb.in.aix.or.jp/~shiraishi/
である。また,Full BASICの代わりにTrue BASICを用いることもできる。その場合,多少,プログラムの修正が必要になる。
[参考文献]
(1) Fractals for the Classroom, Heinz-Otto Peitgen, et al. , Springer-Verlag, 1992
(2)カオスとフラクタル入門,山口昌哉,放送大学印刷教材
(3) 日本工業規格 電子計算機プログラム言語Full BASIC ,日本規格協会,1993
(4) フラクタルの数理,山口昌哉 他,岩波,1993
(5) Introduction to Fractals and Chaos, R.M.Crownover, Jones and Bartlet Publishers, 1995
(6) True BASIC (software product), J.G.Kemeny, et al., True BASIC Inc.
(7) 変換幾何入門,那須俊夫,共立出版,1990
(8)Geometric Transformations, M.E.Mortenson, Industrial Press, 1995

![]() 倍の縮小の合成写像, f 2が 点(1,0)を中心とする45°の回転と
倍の縮小の合成写像, f 2が 点(1,0)を中心とする45°の回転と![]() 倍の縮小の合成写像である場合を考察する。
倍の縮小の合成写像である場合を考察する。![]() )*scale(
)*scale(![]() ), f 2 = shift(1,0)*rotate(
), f 2 = shift(1,0)*rotate(![]() )*scale(
)*scale(![]() )*shift(1,0)
)*shift(1,0)![]() z
z ![]()
![]() + 1
+ 1![]() から
から![]() ,y座標の範囲が
,y座標の範囲が![]() から1までとなる座標系を設定している。描画領域の形状は正方形であるので,x座標の幅とy座標の幅とが等しくなるようにしてある。
から1までとなる座標系を設定している。描画領域の形状は正方形であるので,x座標の幅とy座標の幅とが等しくなるようにしてある。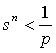 となるようにnを選ぶことが一応の目安になる。
となるようにnを選ぶことが一応の目安になる。![]() z ,
z ,![]()
![]() + 1
+ 1
![]() z ,
z ,![]()