初期の基底解の組合せを簡単に決められない時の対処法初期の基底解の組合せを簡単に決められない時の対処法
一般の線形計画問題をシンプレックス法が適用できるように正規形に変形しても,そのままでは初期基底解を簡単に求められない時がある.
次の例題を考えてみよう．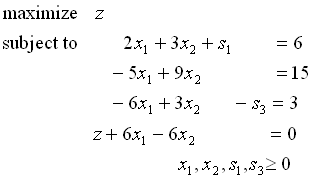
→正規形に変形→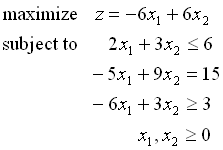
シンプレックス表を作ってみる．
初期の基底変数を決めてみよう．
初期の基底変数を簡単に見つけられない時は2段階シンプレックス法を利用する.
2段階シンプレックス法の概要与えられた線形計画問題をシンプレックス法が適用できるように正規形に変形する.
制約条件においてプラス係数のスラック変数を持たない式に，非負の人工変数(artificial variable)を導入する．
目的関数は人工変数のみからなり，その係数は−１とする．
目的関数を最大化する．
（初期の基底変数は簡単に求まる）
最適値が０ならば第2段階に進む．それ以外の時は，元々の問題に実行可能解は存在しない.つまり，解なし.
第1段階で最終的に得られた表から人工変数を取り除いた制約式を作る.
目的関数は元の問題（最大化問題）の目的関数．
（初期の基底変数は簡単に求まる）
(終了)
例題を使って，その動きを見てみよう.
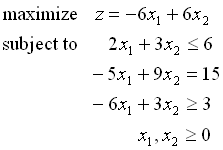
ステップ1：初期基底解を見つけるための線形計画問題を作る
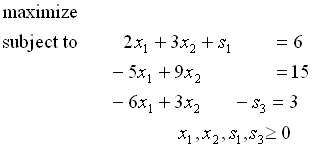（制約条件式のみ考える）
制約条件式の第2・3行目にはプラス係数のスラック変数が存在しない.
↓
人工変数t1,t2を導入する.
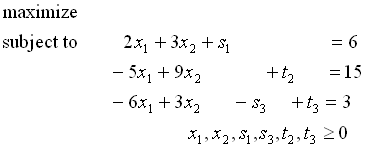
目的関数を定める．
初期基底変数はs1,t2,t3となる．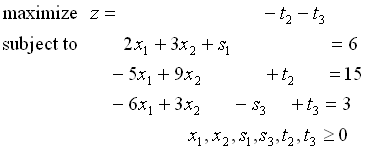
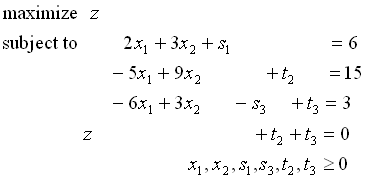
ステップ2 目的関数から初期基底変数になる変数をなくす.
（ｚ行）−(制約条件式2行目)−(制約条件式3行目) より
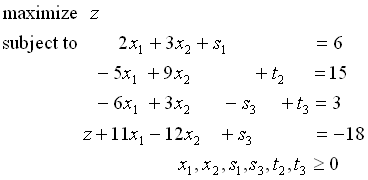
（どうしてこの操作が必要なのだろう？？）
ステップ3 シンプレックス法を用いて上記の線形計画問題を解く．
初期のシンプレックス表
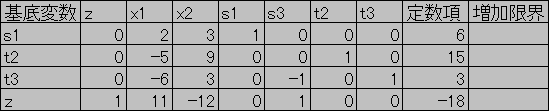
（途中省略）
最終的なシンプレックス表
最適値が０なので，元の問題には実行可能解が存在する(どうしてなんだろう?) 第2段階へ
ステップ1： 元の問題と本質的に同等の線形計画問題を作る
↓
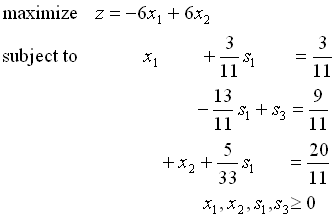
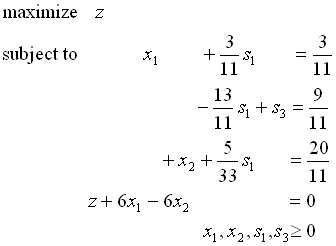
初期の基底変数はx1,x2,s1になる．
ステップ2： 目的関数から初期基底変数を除く
(ｚ行)−６×（制約条件式1行目）＋６×（制約条件式2行目）
↓
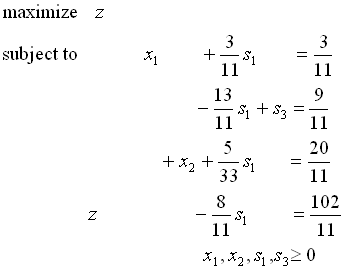
ステップ3： シンプレックス法を適用する
初期のシンプレックス表
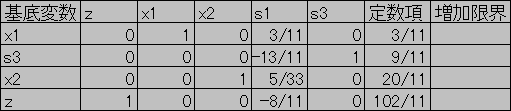
（途中省略）
最終的に得られるシンプレックス表
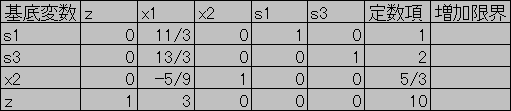
よって，例題の最適解は x1=0,x2=5/3で，最適値は10となる．
（１）
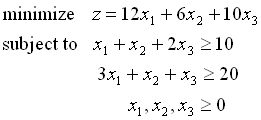
（２）
