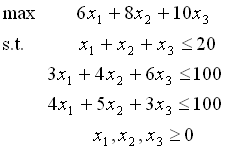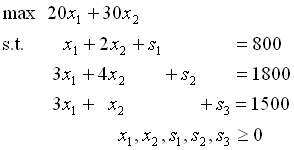
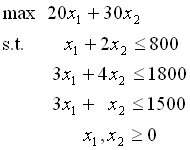
| このHTML版では,講義で配布・使用したしたテキストを完全に再現できませんでした.HTML記述の関係で理解しづらい個所が残っていることをお許しください. | ||
線形計画問題を解く手法の一つであるシンプレックス法の基本的な流れを解説する.シンプレックス法という解法のアルゴリズムは以下のように記述できるが,以下の記述をいきなり読んでも難解なので,とりあえずはその下の例題に取り組んでみよう.
その1.与えられた線形計画問題を正規形に変形する.
その2.正規形に変形された問題の目的関数をzとおく.
その3.zを最大化する線形計画問題に変形する.
(準備終了)
ステップ1.初期設定
ステップ1‐1.シンプレックス表を作成する.
ステップ1‐2.基底変数を式の数だけ定める. ただし,zは必ず基底変数に選ぶ.
ステップ2.現在の基底変数から得られた連立方程式の解が最適かどうか吟味する. 最適ならば終了.最適でない時はステップ3へすすむ.ステップ3.より良い目的関数値を持つ解を見つけるように基底変数と非基底変数の組合せを変更する.
ステップ3‐1.新たに基底変数に仲間入りさせるべき変数を非基底変数の中から選ぶ.
ステップ3‐2.基底から追い出す変数の決定.
ステップ3‐3.新しい基底変数での連立方程式を解く.解を得られた後,ステップ2に戻る.
次の線形計画問題を解きなさい.
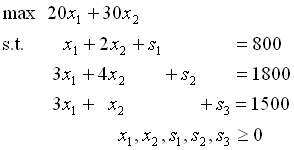
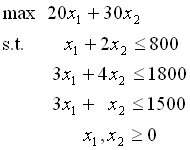
シンプレックス法を適用するための準備準備
その1.与えられた線形計画問題を正規形に変形する
その2.正規形に変形された問題の目的関数をzとおく.
その3.zを最大化する線形計画問題に変形する.
(準備終了)
シンプレックス法の手順ステップ1‐1.シンプレックス表を作成する.(以下参照;準備で得られた線形計画問題の係数を表にまとめたもの.)ステップ1‐2.基底変数を式の数だけ定める. ただし,zは必ず基底変数に選ぶ.
(この後に連立方程式を解かなくてはならないので,なるべく連立方程式の計算が楽になるような基底変数を定める.)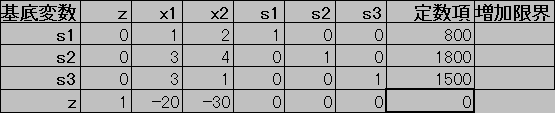
| 解説:z,s1,s2,s3を基底変数に選ぶことにより容易に選られた連立方程式の解 (z,x1,x2,s1,s2,s3)=(0,0,0,800,450,1500)は,すべての値が非負なので,線形計画問題の実行可能領域における端点の一つに対応する.つまり,(x1,x2)=(0,0)は実行可能領域の端点で,その時,目的関数値z=0であることがシンプレックス表からわかる. | ||
ステップ2.現在の基底変数から得られた連立方程式の解が最適かどうか吟味する.
- 現在非基底変数になっている変数の中で, 値を0から正の数に増加させた場合に,目的関数値を増加できるような変数が存在したら現在得られている解は最適ではない(スッテプ3へ進む).もしも,そのような変数がなければ,現在の解が最適解で,zの値が最適値である(最適解が得られたので終了).
| 現在の解が最適かどうかを簡単に判別する方法: シンプレックス表の一番下の行(zが基底変数になっている行)を見る.この行の値がすべて正ならば,現在の解が最適解である.もしも,負の値が存在すれば,それが存在する列の変数を0から正の数に増加させることにより,現在より大きな目的関数値を得ることができる. |
||
 |
||
一番下の行を見るとx1,x2の列に負の値がある.よって,現在得られている解は最適ではない. |
||
注意(陽関数と陰関数):
- 陽関数
- 陰関数
表現が異なるだけ.シンプレックス法では目的関数を陰関数で扱っている.
ステップ3 より良い目的関数値を持つ解を見つけるように基底変数と非基底変数の組合せを変更する.
(実行可能領域の別な端点を探索する.)
ステップ3‐1.新たに基底変数に仲間入りさせるべき変数を非基底変数の中から選ぶ.候補となる変数が複数存在する場合は,最も効果の高い変数を基底に選ぶ.
| 新たに基底に入れる変数の簡単な選び方: 一番下の行(zの行)で最も小さい負の値を持つ列に対応する非基底変数を新たに基底に入れる変数に選ぶ. |
||
 |
||
解説: 仮に現在0であるx1を1つ増やせば目的関数値を30増やすことができ, x2を一つ増やせば目的関数値を20増やすことができる.どちらを増やしても(新たに基底変数に選んでも)目的関数値を増加できるが,単位当たりの増加量が大きいx1を新たに基底に入れる変数として選択する. |
||
ステップ3‐2.基底から追い出す変数の決定.
ステップ3‐1で新たに基底に入れるべき変数を決定したが,基底に指定する変数の数は式の数に固定してあるので,現在の基底の中から追い出す(非基底変数にする)変数を決めなくてはならない.ただし,新たな基底変数の組合せが実行可能領域の端点に対応するように選ばなくてはならない.
| 基底から追い出す変数の簡単な決め方: 一番下の行(zの行)を除き各行において(定数項の値)÷(新たに基底に入れることになった変数の係数)を計算する. その値を増加限界と呼ぶ.各行の増加限界の中で非負で最小の値を取った行に対応する変数を追い出す変数に決める. |
||
 |
||
解説(増加限界の意味) x2の代わりに現在基底変数になっているs1,s2,s3のいずれかの変数を非基底変数にしなくてはならない(zはいつでも基底変数になる.なぜか?).増加限界はx2の代わりに各基底変数を非基底変数に変更した場合に得られる連立方程式における各変数の解を示している(確認してみよう).よって,増加限界が負の値を取る変数を非基底変数にすると,この後得られる解が実行可能解でなくなってしまう. ところで,変数x2を基底変数にする代わりに変数s1を非基底変数にすると実行可能領域の端点が得られる.ところが,変数x2を基底変数にする代わりに変数s2またはs3を非基底変数にすると,ある変数の非負性が崩れてしまう(確かめてみよう!).つまり,いい加減に基底変数の組合せの変更を行うと実行可能領域の端点をうまく見つけることができなくなる.このような不都合が起きないようにするには,新たに非基底変数になった変数の値が0からなるべく急激に増加しないように選べばよいことが計算するとわかる(やってみよう!).つまり,増加限界の値が非負で,かつ,最も小さい変数を新たに非基底変数にすると上記のような不都合は生じないことがわかる. |
||
ステップ3‐3.新しい基底変数での連立方程式を解く.実行後はステップ2に戻る.
| 簡単な新しい基底での連立方程式の解き方: (1)新たに基底に加える変数の列と基底から追い出す変数の行との交点の係数をピボットにする. (2)ピボットを中心に掃き出しを行う. |
||
| 具体的には (1) ピボットが1になるように,ピボットのある行のすべての数字をピボットの数字で割る. |
||
 |
||
具体的には (2) 各行からピボットの行を何倍かして引くことにより,ピボット列の数字がピボット以外0になるようにする. |
||
 |
||
z,x2,s2,s3を基底変数に選んだ時の連立方程式
|
||
| 解説: 掃き出しにより,z,x2,s2,s3を基底変数に選んだ場合の連立方程式の解 (z,x1,x2,s1,s2,s3)=(12000,0,400,0,200,1100)は容易に得られる.また,解は非負なので実行可能領域の端点に対応している.つまり,(x1,x2)=(0,400)は実行可能領域の端点であり,その時の目的関数値は12000となる. |
||
ステップ2.現在の基底変数から得られた連立方程式の解が最適かどうか吟味する.
一番下の行を見るとx1の列に負の値がある.よって,現在得られている解は最適ではない.(ステップ3へ)
ステップ3 より良い目的関数値を持つ解を見つけるように基底変数と非基底変数の組合せを変更する.(実行可能領域の別な端点を探索する.)
ステップ3‐1.新たに基底変数に仲間入りさせるべき変数を非基底変数の中から選ぶ.
候補となる変数が複数存在する場合は,最も効果の高い変数を基底に選ぶ.仮に現在0であるx1を1つ増やせば目的関数値を30増やすことができるので新たに基底に入れる変数とする.
ステップ3‐2.基底から追い出す変数の決定.
増加限界を計算し,最も小さい値となったs2を追い出す変数に決める.
ステップ3‐3.基底の変更を実行する.実行後はステップ2に戻る.
(1)
(2)

z,x2,x1,s3を基底変数に選んだ時の連立方程式.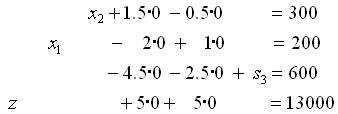
掃き出しにより,z,x1,x2,s3を基底変数に選んだ場合の連立方程式の解 (z,x1,x2,s1,s2,s3)=(13000,200,300,0,0,600)は容易に得られる.また,解は非負なので実行可能領域の端点に対応している.つまり,(x1,x2)=(200,300)は実行可能領域の端点であり,その時の目的関数値は13000となる.
ステップ2.現在の基底変数から得られた連立方程式の解が最適かどうか吟味する.一番下の行を見ると負の値はない.つまり,これ以上基底を変更してもより良い目的関数値は得られない.よって,現在得られている解が最適である.
(終了)
| 注意:ここで紹介したシンプレックス法は基本的な流れを示したもので,これだけでは有限時間内に最適解が求まらない時がある.(どんな時だろう?).必ず有限時間に終了できるシンプレックス法の詳しい内容は次のステップで取り上げる.とりあえずは基本をマスターしよう. | ||
演習以下の線形計画問題をシンプレックス法で解いてみよう.
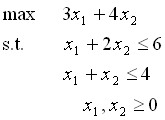
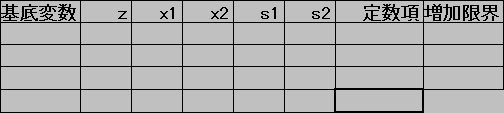
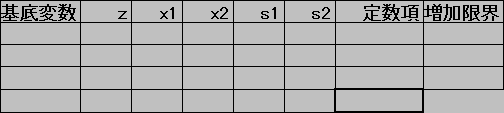
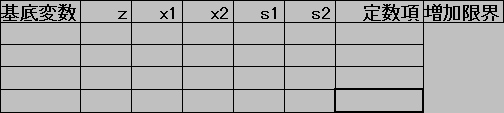
(2)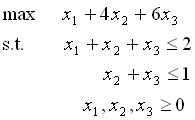
シンプレックス表を数字で埋めていこう.




(3)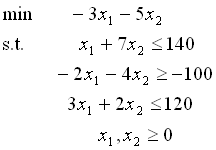
(4)