1.1 SETS AND ELEMENTS
1.2 UNIVERSAL SET, EMPTY SET
1.3 SUBSETS
1.4 VENN DIAGRAMS
1.5 SET OPERATIONS
1.6 ALGEBRA OF SETS, DUALITY
1.7 FINITE SETS, COUNTING PRINCIPLE
1.8 CLASSES OF SETS, POWER SETS
1.9 ARGUMENTS AND VENN DIAGRAMS

発表者　三木田
（本文）
　The concept of a set appear in all branches of mathematics.

The objects comprising the set are called its elements or members.

The statement "p is an element of A"　

"p belongs to A" is written

The negation of p ∈ A is written p ∈/ A.

　数学のすべての分野に集合の概念があります。

集合を構成するものを要素、メンバーと呼ぶ。

ｐがＡの要素の状態

"p belong to A"と読み、書くと

発表者　木村
（本文）
The menbers of all sets under investigation usually belong to

some fixed large set called the universal set or universal set of discourse.

We will let the symbol

For example, in human population studies the universal set consists of all
the people in the world.

The set with no elements is called the empty set or null set

and is denoted by

母集団のすべての要素をが含まれるとき、ユニバーサルセットと呼び

例えば、人間の人口　Ｕ　世界の人々

集合になんの要素が無いときは、エンプチィセット　φ　と書く

発表者　伊藤

（本文）
　If every element in a set A is also an element of a set B,

then A is called a subset of B.

we also say that A is contained in B or that B contains A.

This relationship is written

　Ｂのすべての要素が集合Ａに含まれるとき、

A is contained in B or that B contains A.

となり、 Ａ⊂Ｂ　or 　B⊃Ａと書かれる。

発表者　三木田
　ベン図について

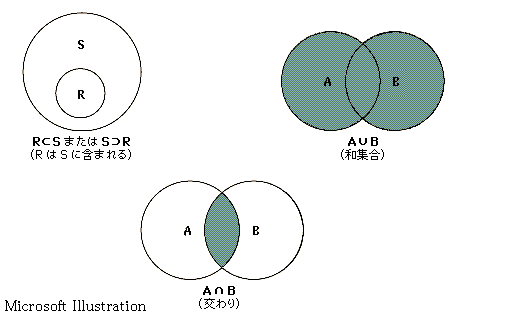
The union of two sets A and B is the set of all elements which belong to A or to B:

The intersection of two sets A and B is the set of elements which belong to both A and B:

The relative complement of set B with respect to a set A or, simply,the difference of

A and B is the set of elements which belong to A but which belong to A

but which do not belong to B:

The aboslute complement or, simply, complment of a set A,

is the set of elements which belong to ∪ but which do not belong to A: