![]()
![]()
情報学部経営情報学科 小川幸子
![]()
1.始めに
私は現在大学に原付自転車で通学しています。大学1年から現在までの4年間の通学で、たびたび道路が自動車で混雑している場面にでくわしました。大学前の道路は混雑が多く、また道路の幅が狭く、自動車を追い越すのも容易でないため、不快に思うことがありました。この不快を解消、又は解消とまではいかなくても、減少させることはできないかと思い、茅ヶ崎市内の渋滞の緩和を研究テーマにしました。
研究テーマを決定しても、具体的にどう取り組んでいくか、悩み、交通に関する論文や本を濫読してしまいました。悩んだすえ、取り組み方を決定しても、漠然としていて、曖昧な点が多く、すぐに研究に行き詰まってしまいました。私は問題を明確にとらえる前にアプローチ方法を考えるという矛盾した行為により、一歩も進めなくなっていました。精神的に不安定な状態におちいり、何度もあきらめかけました。現在の交通状況を把握することは自分では楽観的にすぐできる事なのではないかと思っていましたが、この道路は混んでいるくらいはわかっても、どの程度なのかという明確な数値データの資料などはなく、自分が漠然ととらえている感情を(混雑しているという不快感)を他人にもわかるように数値データとして、具体化するという事の難しさを感じました。
![]()
2.茅ヶ崎市の道路交通状況
私は”道路は自動車で渋滞している”と感じていました。けれど、これは私の感覚だけであり、誰もがそう感じることではないかもしれない。では、実際に茅ヶ崎市内の道路交通状況をどのようなものなのか具体的に把握するため、市の資料で調べてみました。
大きな特徴を以下に述べます。
・自動車交通は38%が都市内、62%が隣接都市間との交通であり、又、乗用車保有台数が神奈川県の平均より高く、都市活動を支え る重要な交通手段となっている。
・幹線道路上では、茅ヶ崎市に発生集中する交通(内々+内外)の3割に相当する通過交通量が流れている。
通過交通量とは、例えば藤沢から平塚への移動のためだけに茅ヶ崎市を通るだけの交通量である。
・実態調査で観測された道路交通量は茅ヶ崎市の主たる幹線道路の容量を越えている状態で大きな混雑状況を起こしている。
茅ヶ崎市を中心とする自動車交通量

![]()
3.渋滞の定義
私は単純に感覚で道路に自動車が多ければ、渋滞が起きているのだと思っていました。しかし、渋滞の意味を調べると、流れがスムーズに行かず、仕事(物・人)がつかえる事と書いてありました。では、どの程度自動車がつかえたら渋滞とするのか、渋滞とはいったい何をもって渋滞が起きていると判断するのか基準を考えました。自動車が連なっている距離で渋滞を定義すると、自分がそれによりどれだけ不快感を感じるか、わかりづらかったため、自動車の走行速度を基準にする事にしました。しかし研究を始めるにあたって、具体的に自動車がどの程度の走行速度がわからなかったので、自分の感覚で時速20km/時以下の状態が15分以上続くことを渋滞と定義して研究をすすめてみました。しかし、7の交通量と走行速度の関係のところで、実際に走行速度を測定したところ、15分以上20km/時以下で走行し続ける事は、ごくわずかということがわかったため、時速20km/時以下の状態が5分以上続く状態を渋滞と定義しました。
![]()
4.渋滞の要因
いったいなぜ、渋滞が起こるのか、その要因ではないかと考えたことを以下に述べます。
・道路のつくりに問題がある。
交通需要が明らかに多いと感じられる道路でも1車線であることや、駅前は一方通行が多く不便なことから考えられます。また、幅の狭い道路が多く、そのため幅の広い道路に交通量が流れやすいと思われます。
・信号の変わる時間、タイミングが悪い。
・違法駐車など交通マナーが悪い。
駅前のような幅の狭い道路や交差点付近で駐車している自動車をよく見かけます。違法駐車している自動車をよけるため、その道路を使用するドライバーは徐行しなくてはいけなくなり、自動車の流れをさえぎっていると思われます。
・ある時間帯に交通量が集中して発生している。
同じ道路でも、時間帯によって、混雑している時としてない時があることから考えられます。
渋滞の要因は他にも様々考えられますが、私は4番目に述べた要因に着目し、そこから解消(緩和)方法を見つけられないかと考えました。
![]()
5.交通量の傾向
4で、ある時間帯に交通量が集中して発生していると述べましたが、では具体的にどの程度交通量が集中して発生しているか、時間別に交通量の傾向調べてみました。交通量のデータは市が測定したデータを使用させていただきました。
5-1交通量の測定方法
40箇所の交差点(下の茅ヶ崎市の道路の図)において、平日、晴天という条件で午前7時から午後7時までの合計12時間の間、1時間間隔で自動車の台数をカウントするもので、自動車のカウントは自動車の走行方向別、交差点への流入、流出別に行なわれました。
以下に流入、流出をもう少し詳しく説明します。
・流入:測定断面(下の交差点の図)をでて交差点内に入っていく自動車の台数をカウントする事。
・流出:交差点をでて測定断面に入ってくる自動車の台数をカウントする事。
| 交差点 | 茅ヶ崎市の道路 | ||
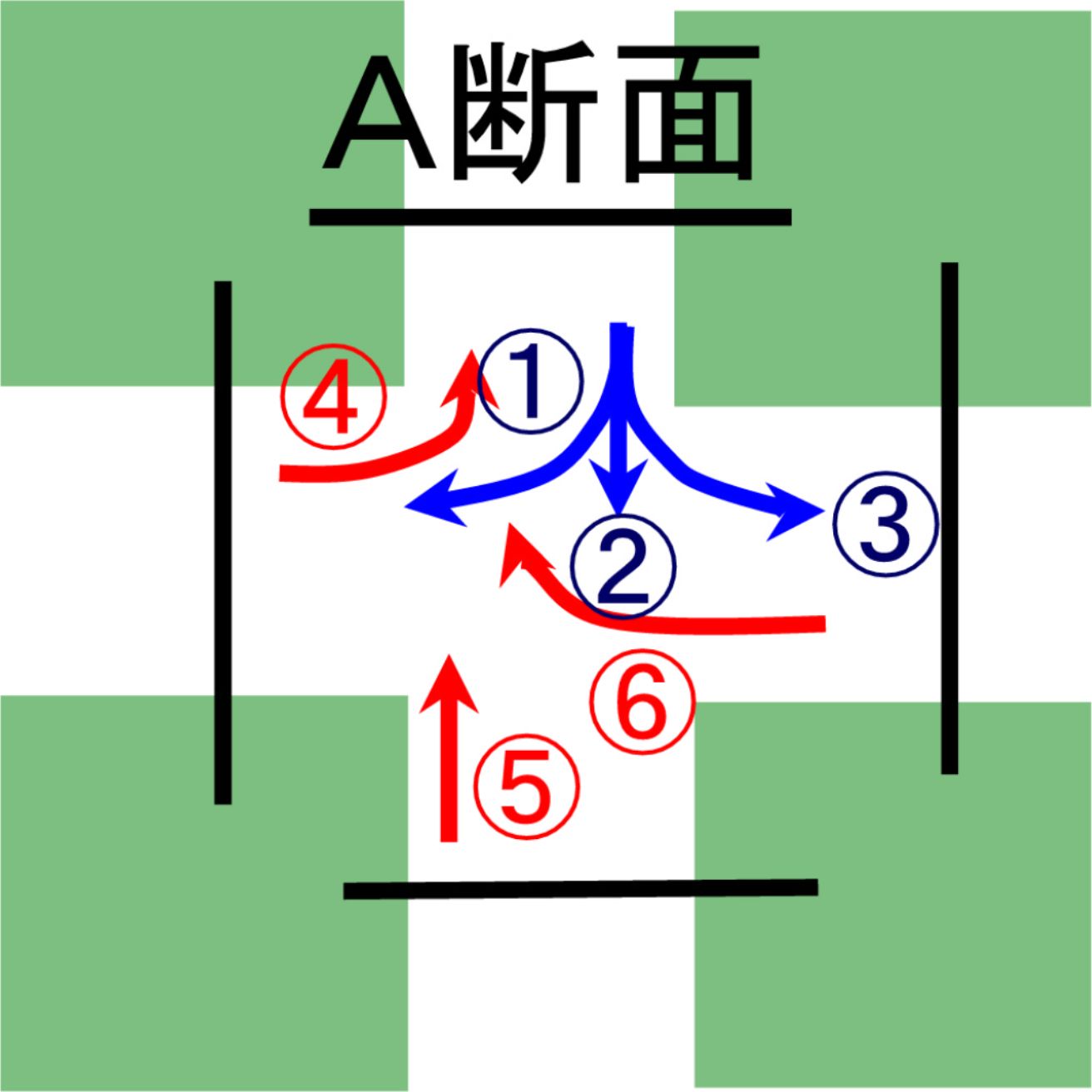 |
A断面流入:1+2+3 A断面流出:4+5+6 (矢印は車の進行方向) |
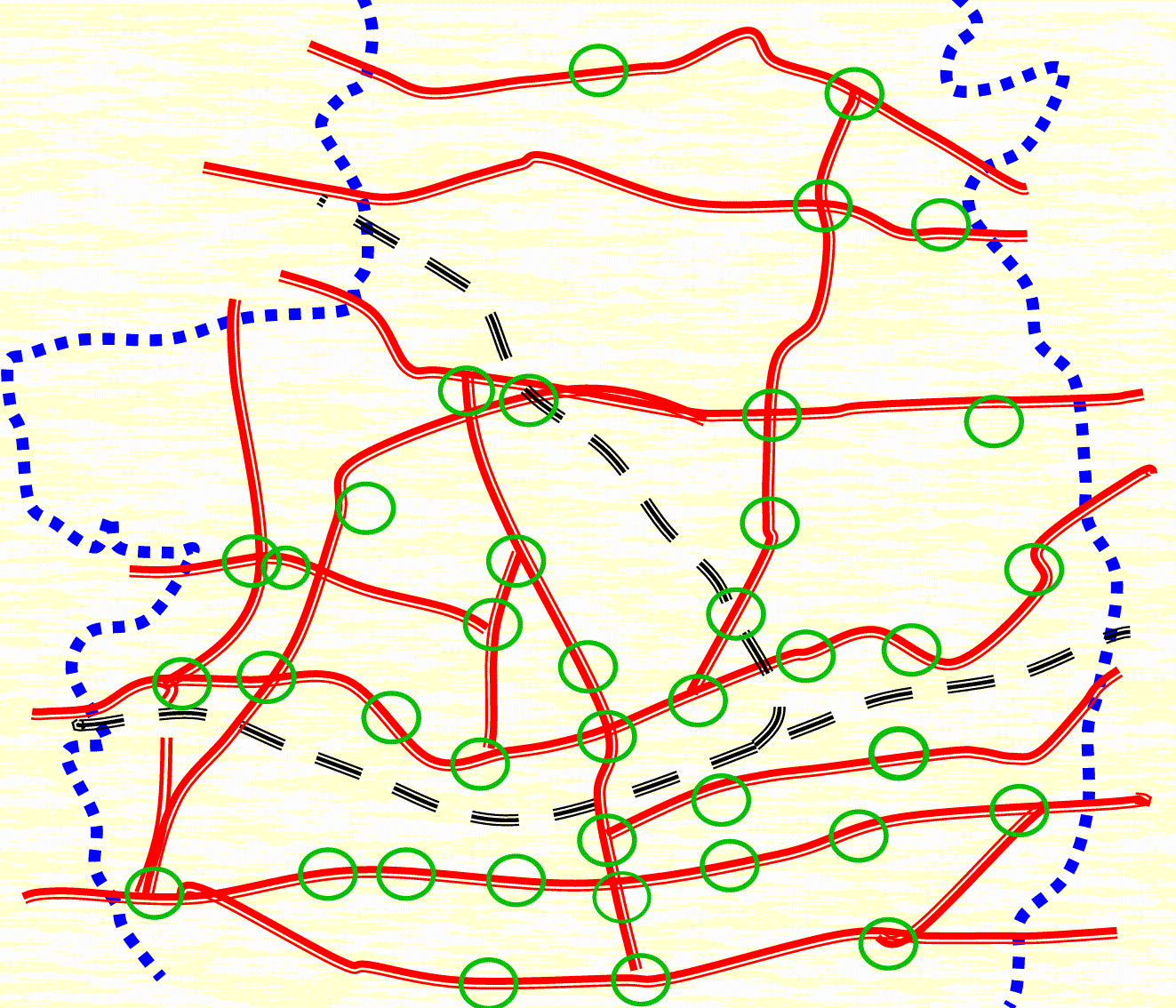 |
交通量測定地点 (丸の位置40箇所において測定) |
茅ヶ崎市の道路は主要と思われる道路のみを、簡略化させていただきました。
1箇所の交差点に1~5箇所の測定断面が(十字路なら4箇所)あるため、測定断面は153箇所あり、流入、流出をあわせると(一方通行を抜かし)302の交通量のデータになります。
5-2交通量の傾向の分析方法
行なった分析方法を以下1~3に示します。
1.5-1の302の交通量のデータをエクセルに入力し、交通量の時間別の変動を知るため、各個所の標準偏差を出します。交通量がある時間帯に集中しているということは、、たいした交通量が発生してない時間帯もあるという事なので、時間により交通量が散らばっているという事になります。そこで、この散らばりの尺度として標準偏差を使用することにしました。
<標準偏差>
散らばりの尺度として、最も広く使われるのが、各観測地と平均の差(観測地が平均からどれだけ離れているかを表し、これを偏差(deviation)と呼びます。)に基づくものです。偏差は正負いずれもとりますので(ただ単に合計しただけでは0となってしまいます)、符号の影響をとり除く為二乗し、その合計をn(データの数)で割ったものが分散(variance)です。分散は偏差を平方したものの平均ですので、このままでは直接もとのデータと比較できません。(例えば二乗した事によって単位が変わってしまいます。)そこでこの平方根をとったSを標準偏差(standard
deviation)と呼び、分析に用います。
2.各箇所の標準偏差の平均(49.02)を出します。(小数点第3位で四捨五入)この平均を基準とし、時間別交通量の変動率が高いタイプと低いタイプの2つに分類します。
3.各箇所の12時間合計の交通量の平均(4328.87)を出します。この平均を基準とし、②で分類したタイプをさらに混雑が起きているタイプと起きていないタイプに分類します。(交通量が多ければ混雑している可能性も高いため、交通量が多い=混雑が起きているとします。)
上記の方法でタイプ分けした4つのタイプを以下のように図で示します。中央に縦にひかれている点線が混雑の発生基準となる線、横にひかれている線は時間別交通量の変動が大きいか小さいかの基準となる線で、①~④と番号付けしました。
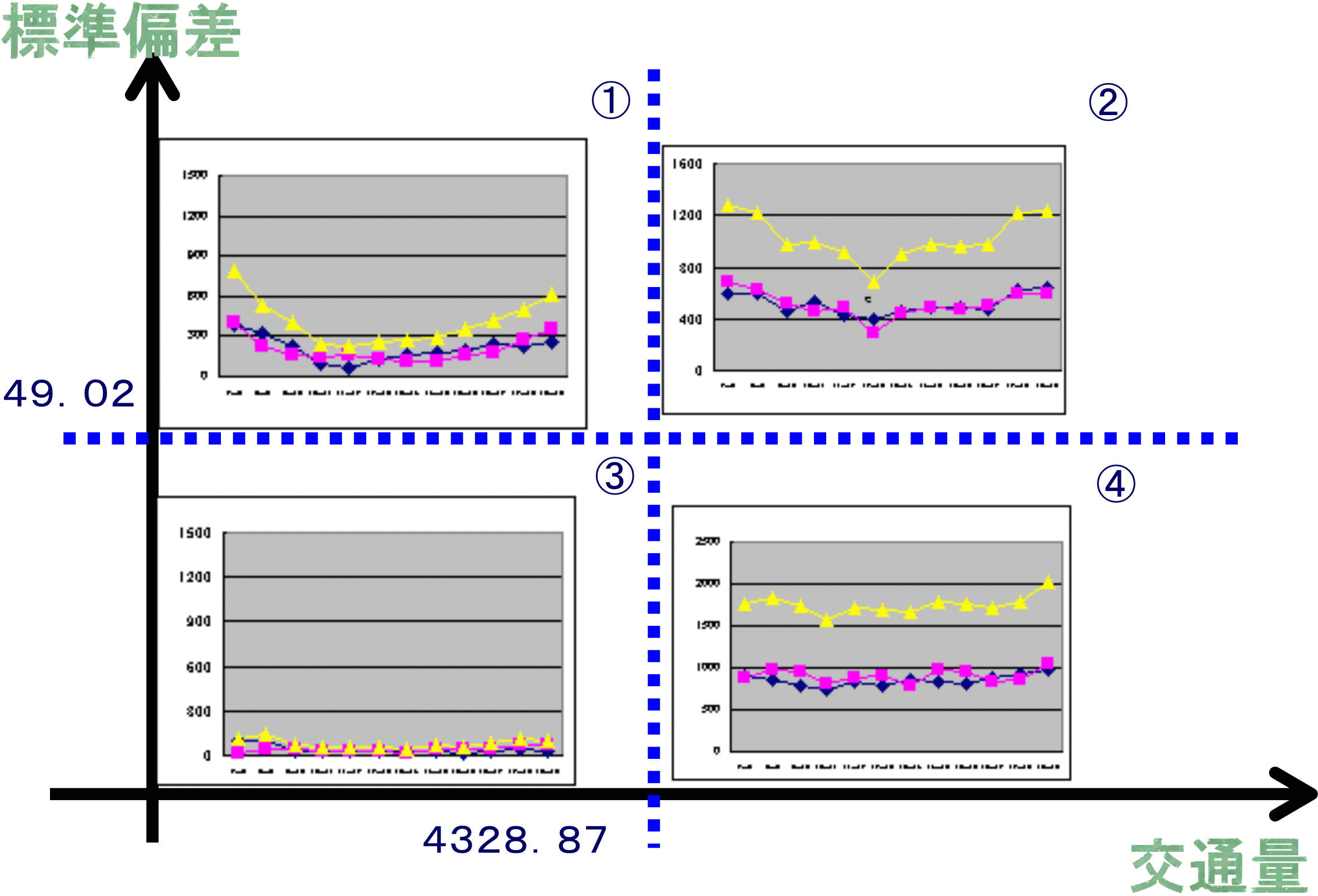
結果
|
①標準偏差>=49.02かつ交通量<4328.87 46箇所 ②標準偏差>=49.02かつ交通量>=4328.87 91箇所 ③標準偏差<49.02かつ交通量<4328.87 140箇所 ④標準偏差<49.02かつ交通量>=4328.87 25個所 |
交通量が極端に少ない個所のデータも入っているため、基準を平均とするのは少し疑問が感じられました。そのため、 極端に少ない箇所のデータを省いてもう一度考えてみることにしました。
12時間合計の交通量が1000台を超えない箇所(28箇所)を抜かしもう一度1~3の作業をしました。標準偏差の平均が52.76になり交通量の平均が4734.71になり、次のような結果に変わりました。
結果
|
①標準偏差>=52.76かつ交通量<4734.71 54箇所 ②標準偏差>=52.76かつ交通量>=4734.71 79箇所 ③標準偏差<52.76かつ交通量<4734.71 120箇所 ④標準偏差<52.76かつ交通量>=4734.71 21個所 |
この結果、以下の図のようになりました。
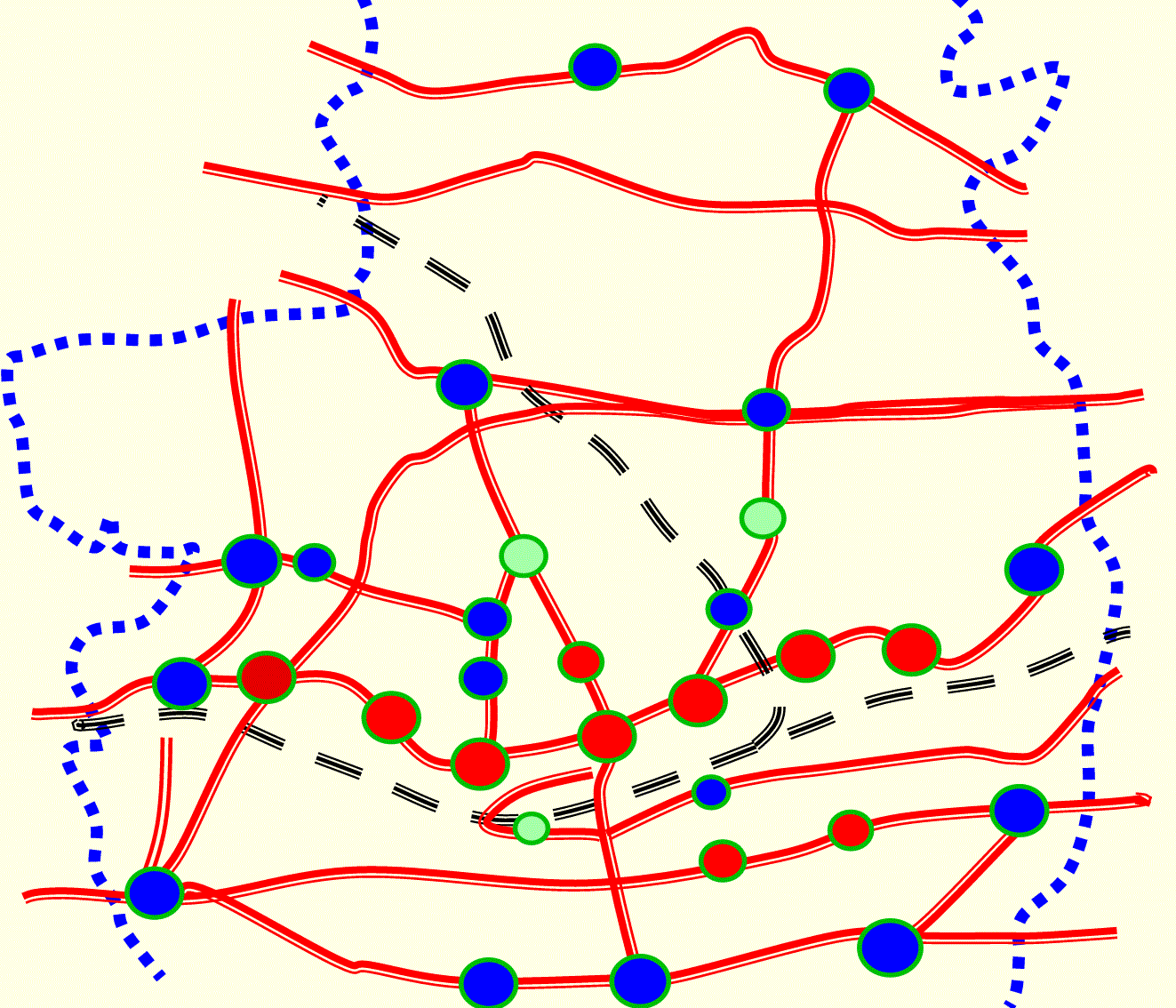 |
国道1号線(図の②、④両タイプの交差点が連なっている道路)においては、当初の予想通りの結果になりましたが、国道134号線(図の一番下の道路)においては、交通量の変動が大きいという意外な結果になりました。40箇所の交差点のうち、31箇所の交差点が②、④のタイプに含まれ、主要道路はほとんど問題を抱えている状態となりました。
![]()
6.緩和方法
渋滞が発生するの可能性が高いのは交通量が多い②、④のタイプとし、①、③タイプは渋滞が発生しないとし、除外して緩和方法を考えました。②は時間別交通量の変動が大きいのだから、ある時間帯に交通量が集中していると考えられるため、交通量が集中している時間帯の交通量だけを渋滞が発生するという基準値を決め、基準値以上の交通量を前(または後ろ)に1時間ずらす事で、交通量を分散させ、解消(緩和)する方法を考えました。これは、交通量が集中して発生する時間帯にその交差点を流入、流出しているドライバーの何%かの出発時刻を1時間ずらせたと仮定して行ないます。④のタイプに関してはこの方法では、効果は望めないと思ったのですが、他にいい案も浮かばなかったため、この方法を試してみる事にしました。基準値を渋滞が発生する交通量としたので、その交通量を知るため、渋滞の判断基準となる走行速度と交通量の関係を考えました。
![]()
7.交通量と走行速度の関係
走行速度の測定方法
いろいろと考えたのですが、いい方法が浮かばなかったため、実際に原付自転車を運転して、走行速度を測定する事にしました。平日、晴天の日の午後3時から午後7時の条件で5分間(時速20km/時以下の状態が5分以上続く状態を渋滞と定義したため)運転して、距離をメーターで測り平均時速を測定しました。
測定した道路は②のタイプからは文教大学前(茅ヶ崎市の道路の図一番上の道路)の道路、④のタイプからは国道1号線を選びました。測定した結果、国道1号線に関しては、交通量と走行速度の関係がまったくみられない不思議な結果になってしまい、文教大学前の道路は以下のような結果になりました。
結果
| 平均 | |||||||||
| 交通量(台) | 467 | 470 | 486 | 507 | 593 | 595 | 631 | 638 | 548.375 |
| 時速(km/時) | 16.2 | 31 | 31 | 24.8 | 9.6 | 20.4 | 20.4 | 19.2 | 21.575 |
この測定結果から交通量と走行速度の関係を知るために回帰分析を行ないました。回帰分析(regression
analysis)は、2変数x,yの二次元データがあるとき、yをxで定量的に説明する回帰方程式(regression
epuation)と呼ばれる式を求めることを目的としています。交通量が走行速度にどう影響を受けるか、時速を説明する変数x、交通量を説明される変数yとします。
回帰方程式から時速20km/時と時速40km/時の時の交通量を予測して、以下のようになりました。
| 時速(km/時) | 20km/時 | 40km/時 |
| 交通量(台) | 556.5829345 | 452.3551952 |
![]()
8.緩和結果
7の走行速度と交通量の関係で渋滞の発生基準になる走行速度時速20km/時の時の交通量と、走行速度時速40km/時の時の交通量を予測しました。走行速度時速40km/時の時の交通量も予測したのは走行速度時速40km/時の交通量をその道路の容量とし、まったく不快感を感じない、適した交通量ではないかと考え、その道路がどれだけ容量を越え、不快感を与えるかも表したいと考えたからです。そして、容量を1、他の時間帯の交通量÷容量=混雑度とし、この混雑度が1以上で大きくなるにつれ、不快感が大きくなるとします。
混雑度を計算し6の緩和方法を行なった結果、以下のようになりました。
| 20km/時 | 40km/時 | |
| 混雑度 | 1.23041119 | 1 |
| 時間 | 流入 | 流出 | 流入混雑度 | 流出混雑度 | 流入移動台数 | 流出移動台数 |
| 7-8 | 591 | 683 | 1.3065 | 1.5099 | 34.4171 | 126.4171 |
| 8-9 | 588 | 624 | 1.2999 | 1.3794 | 65.8342 | 193.8342 |
| 9-10 | 455 | 519 | 1.0058 | 1.1473 | 156.2513 | |
| 10-11 | 527 | 464 | 1.1650 | 1.0257 | 63.6684 | |
| 11-12 | 433 | 484 | 0.9572 | 1.0700 | ||
| 12-13 | 396 | 296 | 0.8754 | 0.6544 | ||
| 13-14 | 458 | 439 | 1.0125 | 0.9705 | ||
| 14-15 | 487 | 486 | 1.0766 | 1.0744 | ||
| 15-16 | 486 | 470 | 1.0744 | 1.0390 | ||
| 16-17 | 467 | 507 | 1.0324 | 1.1208 | 66.2513 | 25.2513 |
| 17-18 | 631 | 595 | 1.3949 | 1.3153 | 155.8342 | 74.8342 |
| 18-19 | 638 | 593 | 1.4104 | 1.3109 | 81.4171 | 36.4171 |
| 渋滞 |
合計で1080.43台の移動、12時間合計の8.7718%でこの交差点における渋滞は解消される結果になりました。1割以下の人が出発時刻をずらす事で渋滞が解消される結果になったので、私は有効な手段ではないかと思いました。しかし、出発時刻をずらすことが可能という仮定で行なったのですが、実際にどうやって出発時刻をずらすのか、単純に朝、夕に交通量が集中発生している場合、通勤手段に車を利用しているため、集中発生していると予想できるので勤務時間がずれればいいと思ったのですが、どれくらいの会社がどれだけ時間をずらせばいいかということは、ドライバーの出発地点と目的地点を知る必要があるため、現実に可能な方法だろうかという疑問が残ってしまいました。
![]()
8.謝辞
この卒業論文を作成するにあたり、多くの方々のご協力をいただき、厚くお礼申し上げます。データ収集の際協力してくださった茅ヶ崎市役所の職員の方々大変お世話になりました。研究に行き詰まり、やめてしまいそうになった時、同研究室の方々、根本先生多大なご迷惑をおかけして、申し訳ありません。大変感謝いたします。誠にありがとうございました。
![]()
参考文献
[1] S60 OD調査 S60センサス
[2] H12 市内主要幹線交通量調査委託報告書
[3] Excelによる統計入門
[4] 第18回交通工学研究発表会論文報告集