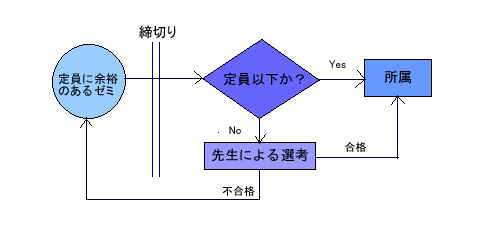
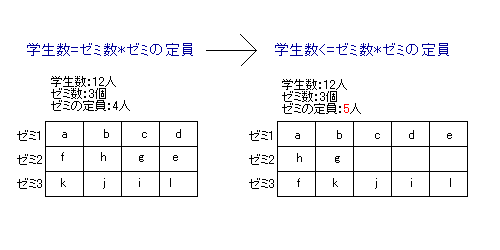
�}1.1���݂̔z�����@�̗���
������w�̃[�~�z�����
������w�@97p21037 ����@�O
97p21037@shoan.bunkyo.ac.jp
�@������w�o�c���w���ł�3�N���ɂȂ�Ɓu�[�~�i�[����i�ȉ��[�~�j�Ƃ����Ȗڂ𗚏C���Ȃ��Ă͂Ȃ�Ȃ���w����10���J�݂��ꂽ�[�~�̒��̈�ɏ������顂��ׂĂ̊w�����s�������[�~�ɏ����ł���������A���ꂼ��̃[�~�ɂ�14�l�Ƃ������������̂ł����͂����Ȃ��B�������̃[�~�ɏ����������Ɗ�]����w����������z�������͑I�l���Ċw�����I��A����������B���ݍs���Ă�����@�́A�w������[�~��I�����Ă����ň�x���ߐ�B����ȉ��Ȃ炻�̂܂����ł��邪������z����Ƃ��̃[�~�̐搶�ɂ���Đ��сA�ʐڂȂǂ���I�l����額��i�Ȃ珊���A�s���i�Ȃ炻�̊w���͍��x�͒���ɗ]�T�̂���[�~����I�ԁA�����Ă܂����ߐ�A�Ƃ����i�K�����ׂĂ̊w������������܂ŌJ��Ԃ��Ƃ������@�ł���
�@���̕��@�ł͑���]�ŕs���i�ƂȂ��Ă��܂����w���́A����ȍ~�͎c�����[�~���炵���I�ׂȂ��B�܂��A�l�C�̂���[�~�Ɋ�]���o�����͊w���ɂƂ��đ傫�ȕ��S�������顎��ہA����]��A�[�~���������A�m����B�[�~�Ɋ�]���o���ď��������Ƃ����b������̊w�ȂŊJ�݂����[�~�́A�o�ρA�o�c�AOR�A��v�ȂǑ���̕���ɂ킽���Ă���̂ŁA����]�ŏ����ł��Ȃ��w���͕s�{�ӂȕ���̃[�~�ɂ�����]���o���Ȃ��Ƃ��������N���肤��
�@���݂̔z�����@�͊w���̑���]�������Q�Ƃ��Ĕz�������āA����]���Q�Ƃ��Ĕz��������A�Ƃ����悤�ɉ��ɔz�����Ă��顂����ŏ��ɂ��ׂĂ̊w���̃[�~�ɑ��鏊�����������Ԃ�m�邱�Ƃ��o����������Ɨǂ��z�����ł���̂ł͂Ȃ����ƍl�����B�����ŁA���z�̔z�����@���Ă��Č��݂̔z�����@�Ɣ�r�����悤�ƍl�����B���݂̔z�����@�̓������l�����A���z�̔z�����@�Ƃ��Ĉ��茋������K�p�����
�@������w�ł�3�N���ɂȂ�ƁA�K���[�~�ɏ������Ȃ��Ă͂Ȃ�Ȃ��B���ׂ̈Ɋw���̃[�~�z�����s����B�[�~��15�J����Ă��āA���ꂼ��̃[�~�̒����14���A�w���͖�180���ł���B
�@ 2�N���̏H������w���̓[�~�̌��w��A�搶���ւ̖K��Ȃǂ��s���A�����������[�~��1�����I������B�����đI�������[�~��p���ɋL������o����B���̊�]��̃[�~������ȉ��Ȃ炻�̂܂����ł���̂����A����������Ă���Ƃ��̃[�~�̐搶�ɂ���Đ��сA�ʐڂȂǂɂ���Ċw���͂ӂ邢�ɂ�������B�����ŕs���i�ƂȂ��ă[�~�ɏ����ł��Ȃ������w���́A���x�͎c�����[�~���珊���������[�~��I������A�Ƃ����z�����@�����ׂĂ̊w������������܂ōs���Ă���i�}�P�Q�Ɓj�B

�}1.1���݂̔z�����@�̗���
�@�o�c���w�Ȃł͌o�c�A��v�A�o�ρAOR�A�@���A�ȂǕ��L������̃[�~���J�݂���Ă���B���ׁ̈A���݂̔z�����@�ł͑�1��]�ɏ����ł��Ȃ������w���́A�����̕�����������̃[�~�Ɋ�]���o���Ȃ����Ƃ��N����B�Ⴆ�A�o�c�Ɋւ��邷�ׂẴ[�~����1��]�Œ���������ꍇ�A�o�c�Ɋւ��镪��ɑ�2��]���o���Ȃ��Ƃ������Ƃł���B���̎��͕s�{�ӂȃ[�~�ɏ������邵���Ȃ��̂ł���B�܂��A�{���͐l�C�̂���[�~����1��]�����ǁA���̃[�~�Ɋ�]���o�����m���ɏ����ł����2��]�̃[�~��I������Ƃ������Ƃ��l������B�܂�A���̔z�����@�͊w���ɂƂ��ĂƂĂ����X�N���傫���B
�@ �H���ɂ��낢��ȃ[�~�����w���āA�قƂ�ǂ̊w���͂�����x�����������[�~�̏��ʕt���͂ł��Ă���͂��ł���B���������̔z�����@�ł͑�1��]�����Q�Ƃ���Ȃ��B�����A�w���̃[�~�ɑ��鏇�ʕt���Ƃ��������g�����Ƃ��ł�����A�������I�Ȕz�����ł���̂ł͂Ȃ����ƍl����B
�@�����ŁA���̍l���闝�z�I�Ȕz�����@���Ă��āA���݂̔z�����@�Ɣ�r���悤�ƍl����B�����B���z�̔z��������̂ł͂Ȃ��A�����������Ŕ�r������Ƃ����_����A���݂̔z�����@�̓���������ł̗��z�̔z�����@���Ă���Ƃ���B
�@
���̓����Ƃ��āA��������[�~�Ɋւ��Ă͂��̃[�~�̐搶���Ɋw����I���ł��錠�����^������Ƃ������Ƃ���������B���̂��Ƃ���搶�����w���ɑ��ĉ��炩�̊�ŏ��ʕt�������Ă��鎖���킩��B
�@�ȏ�̂��Ƃ���A
�@�@�@�@�@�@���z�̔z���ɂ������Đ搶�̈ӌ����l������Ă���Ƃ�����������������
�@�@�@�@�@�A�w���̃[�~�ɑ��鏇�ʕt��
�@�@�@�@�@�B�搶�̊w���ɑ��鏇�ʕt���A�Ƃ��������A
�Ƃ��������g���ė��z�̔z�����@���Ă���B
�@
�@�z�����Ɋւ��錤����ʂ͐���������[6]�A���̂قƂ�ǂ͉�����i�Ƃ��Đ��`�v���K�p���Ă���B�������A������w�̃[�~�z�����̓������l������Ɛ��`�v��@�������茋������K�p�����ق����ǂ��Ǝ��͍l����B�Ȃ��Ȃ�A������w�ł͔z���ɓ������Ċw���̈ӌ������ł͂Ȃ������̈ӌ����܂܂�Ă��Ă�B�w���A������2�̂ǂ���̃O���[�v�������ł���z����B���ł�����茋�����̕����K���Ă���ƍl��������ł��顂��̏͂ł́A�܂����`�v��@�ƁA���茋�����̍Œ���̐��������āA�Ȃ����`�v��@�ł͂Ȃ��A���茋�����ŗ��z�̔z�����@���Ă���̂��������B
�@���`�v����Ƃ́A���{���̐��`�s�����ɂ���ċK�肳����Ԃ̒��Ő��`�����ŏ����܂��͍ő剻������ł���B
�@�ŏ����܂��͍ő剻������`����ړI���ƌĂсA�ő剻�̎��ɂ�max�A�ŏ����̎��ɂ�min���������B���͈̔͂��K�肷����`�s������s.t.(subject
to)�̌�ɏ����B���ׂĂ̐��`�s���������ϐ��̏W�܂�����s�\���ƌĂԁB���s�\���̑��݂���̈�����s�\�̈�ƌĂԁB���s�\�̈�̒��ŖړI�����ŏ����܂��͍ő剻������̂��œK���ƌĂԁi�}3.1�Q�Ɓj[1]�B
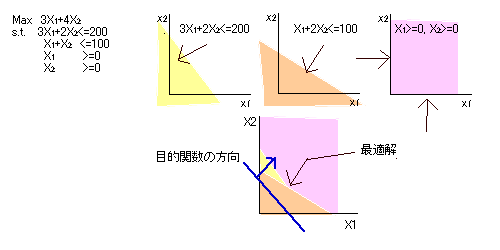
�}.3.1�D���`�v��@�̎��s�\�̈�A�œK���̗�
�@���̐��`�v����[�~���蓖�Ė��։��p����B
�@�\3.1�͊w��i���[�~j�ɏ�������Ȃ�(i,j)�Ԗڂ̃Z����1�A�������Ȃ��Ȃ�0�Ƃ��邱�Ƃ�\���Ă���B�\3.2�̃Z��(i,j)�͊w��i���[�~j�ɏ��������Ƃ��̖����x��\���B���̂悤�ɍl����A�Z���ii,j�j��Xij�Ƃ��āA{0,1}�ϐ��Ƃ��čl���邱�Ƃ��ł���B�܂�莮������Ɛ}3.2�̂悤�ɂȂ�B�@�@�@�@�@�@
�\.3.1�D������\���\
| �[�~1 | �[�~2 | �[�~3 | |
| �w��1 | 0 | 1 | 0 |
| �w��2 | 1 | 0 | 0 |
| �w��3 | 0 | 0 | 1 |
���̗�ł͊w��1�̓[�~2�ɁA�w��2�̓[�~1�ɁA�w��3�̓[�~3�ɏ���
�\.3.2�D�����x��\���\
| �[�~1 | �[�~2 | �[�~3 | |
| �w��1 | 10 | 5 | 2 |
| �w��2 | 10 | 4 | 8 |
| �w��3 | 7 | 6 | 10 |
�w��1���[�~1�ɏ��������10�A�[�~2�ɏ��������5�A�[�~3�ɏ��������2�_�̖����x��������@�@�@�@�@�@�@�@�@
�@
�@�@�@�@�@//�_�����������������x������
max 10X11 + 5X12 + 2X13 +
10X21 + 4X22 + 8X23 +
7X31 + 6X32 + 10X33
s.t.�@//���ꂼ��̊w���͂ǂꂩ�̃[�~�ɏ������Ȃ��Ă͂Ȃ�Ȃ��Ƃ�������
X11 + X12 + X13 >= 1
X21 + X22 + X23 >= 1
X31 + X32 + X33 >= 1
�@�@�@//���ꂼ��̃[�~�͒���ȉ��łȂ���Ȃ�Ȃ��Ƃ�������
X11 + X21 + X31 <=
�[�~1�̒��
X12 + X22 + X23 <=
�[�~2�̒��
X13 + X23 + X33 <=
�[�~3�̒��
�@�@�@//�\3.1�����悤�ɂ���ׁA�ϐ��ɐ����^����
�@�@�@�@�ϐ�X11,X12,�E�E�EX32,X33��{0,1}�ϐ�
�@�@�@�@�@�}.3.2 �z������莮��
�@
�@���̖��ɂ����ē��������̕ϐ���0��1�ł���B���̂悤�ɋ��߂���𐮐��Ɍ��肷����`�v��𐮐��v��Ƃ����B�����v��@�͔��ɓ�����Ƃ��Ēm���Ă��顂������A���̖��̐�������Ō�̐���u�ϐ�X11,X12,�E�E�EX32,X33��{0,1}�ϐ��łȂ���Ȃ�Ȃ��v���u�ϐ�X11,X12,�E�E�EX32,X33��0����1�̊Ԃ��Ƃ�Ηǂ��v�Ɗɘa���Ă��A�œK���̒��ɐ����l�݂̂���Ȃ���̂����݂���[2]�B�����ōŌ�̐����}3.3�̂悤�ɂ���ΐ��`�v��Ƃ��đ����鎖���ł��A��͌v�Z������Γ�����������B
�@�@//�ϐ��ɑ��Ċɘa������
0 <= X11,X12,�E�E�EX32,X33
<= 1
�}.3.3 ���`�v��Ɋɘa
�ȏ�̂悤�ȃA�v���[�`���s���A�[�~�̔z�����s�����Ƃ��ł���B���ׂ̈̏����Ƃ��Ċw���ɂ͏��ʕt���̈ȊO�ɖ����x��\���Ă����Ȃ���Ȃ�Ȃ��B
�@
�@n�l�̒j���W��M��n�̏����W��W�����݂���Ƃ���B�e�l�ِ͈���ΏۂɍD���ȏ��Ԃ������Ă���B����j��h������d�f���d���D�ގ��Ad<hd'�ƕ\���B����ɁAd=d'�̎���d<=hd'�Ə����B�����ɂ����Ă����l�ɕ\������B
�@1�l�̒j��h��1�l�̏���d�̑g�ih,d�j���y�A�ƌĂԁB�������̃y�A����\�������W��M�ɂ����āA���ׂĂ̐l�������ꂩ�̃y�A�ɑ����A���ǂ̐l���ЂƂ�葽���̃y�A�ɑ����Ȃ��Ƃ��AM�̓}�b�`���O�ƌĂ��B�}�b�`���OM�Ƀy�A(h,d)�������Ă��鎞�Ah��d(d��h�j�́i�}�b�`���OM�ɂ�����j�p�[�g�i�[�ƌĂсAh=pM(d)(d=dM(h))�@�ƕ\���B
�@����}�b�`���OM�ɂ����āA�ȉ���3�̏��������ׂĖ������y�A(h',d')�̓}�b�`���OM���u���b�N���Ă���ƕ\�����A���̃y�A���u���b�L���O�y�A�ƌĂԁB
�@�@�@�@�@�@�@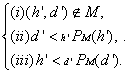
�@�@(h',d')��M�ɂ�����u���b�L���O�y�A
�u���b�L���O�y�A�����݂��Ȃ��}�b�`���O������}�b�`���O�ƌĂԁB
����}�b�`���O��Gale-Shapley�̃A���S���Y���ɂ���ċ��߂邱�Ƃ��ł���B
|
Gale-Shapley�̃A���S���Y�� �����@�j���W��M�A�����W��W�A����ъe�l�ِ̈��S���ɑ���I�D���� �o���@����}�b�`���O step0�@�i�����ݒ�j�S���͓̏Ɛg�ł���A���ׂĂ̒j���͂ǂ̏����ɂ��v���|�[�Y���s���ĂȂ��B step1�@�Ɛg�̒j��h�����݂������ȉ��̑�����J��Ԃ�
|
�@���̃A���S���Y���ł͒j���������Ƀv���|�[�Y��������@���Ƃ��Ă��邪�t�ɏ������j���Ƀv���|�[�Y������Ƃ������@���s���Ă�����}�b�`���O��������B
�@����}�b�`���O�͂����Ȃ���茋�����̗�ɂ����Ă����Ȃ��Ƃ�1�͑��݂��A��ʓI�ɂ͕������݂��Ă���B���̒��̂ЂƂƂ��ē�����Gale-Shapley�̃A���S���Y���̉��̓������ȉ��Ɏ����B�i�ؖ��͏ȗ�����j�@
|
���茋���̂����ɑ�Gale-Shapley�A���S���Y���œ���ꂽ�}�b�`���O��M1�Ƃ���B |
�܂�A�j������v���|�[�Y��������@���Ƃ�Βj���ɂ����Ƃ��D�܂����i�j���ŗǁj�A��������v���|�[�Y��������@���Ƃ�Ώ����ɂ����Ƃ��D�܂����i�����ŗǁj�̃}�b�`���O��������B�@
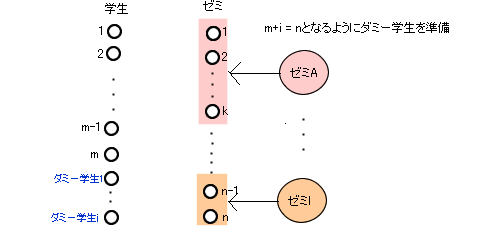
�@�j�����w���A1�l�̏�����1�̃[�~�ƍl����Έ��茋�������[�~�z�����ɓK�p�ł��邪�A�������̖��_����������B�����ł�������A�����z���p�Ɋg������B�w��n�l�ɑ��[�~����m�ł���1��1�̃}�b�`���O�ɂł��Ȃ��A�Ƃ������Ƃ���������B����ɂ��Ă͂���[�~�̒����k�l�Ȃ炻�̃[�~��k�l�̏����Ƃ݂ēK�p����悢�i�}3.4�Q�Ɓj�B
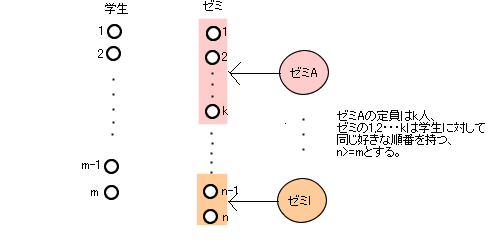
�}.3.4�D���茋�����̔z�����ւ̊g��
�@���̂悤�ɂ���[�~�̏W���̗v�f���͊w���̏W���̗v�f�������Ȃ邩�A����B��ʓI�ɂ͏���̂ŁA�w���̏W���Ƀ_�~�[�̊w�������āA�[�~�Ɗw���̏W�������������Ȃ�悤�ɂ���B���̎��A�_�~�[�̃[�~�ɑ���D���ȏ��Ԃ͓K���ł悢�B�܂��A�[�~�̑I�D�����ɂ����āA�_�~�[�w���̈ʒu���鏇�ʂ͂��ׂĂ̊w���̏��ʕt�����I�������ɂ����悢�B�_�~�[�w�����m�̏��ʂ͓K���ł悢�B�i�}3.5�Q�Ɓj
�}3.5�D���茋�����̔z�����ւ̊g��2�@
�@���̂悤�ɂ���Έ��茋�������[�~�z�����ɓK�p�ł���B
�@������w�ł́A�w���̈ӌ������ł͂Ȃ���������ꍇ�A�搶���̈ӌ����z���Ɋւ���Ă���B���`�v��@�ɂ����āA�ړI�����u�[�~�Ɗw���̖����x���ő�ɂ���v�Ƃ���Ίm���ɐ搶���̈ӌ����܂܂�A���A�����x���ő�ɂȂ�z�����B�������A�S�̖̂����x���ő�ɂ��邽�߂Ɋ��l���̊w���i�[�~�j���s�{�ӂȌ��ʂɂȂ�\��������B�����ŁA�z�����ꂽ����}�b�`���O�ɂ����āA�l�̕s���̂Ȃ��悤�ȃ}�b�`���O�����茋�����Œ�Ă��悤�ƍl�����B�܂���Gale-Shapley�̃A���S���Y���Ŋw���A�������̓[�~�ɍł��L���Ȉ���}�b�`���O�����߂ĕ��͂����āA��������������Ȕz����ڕW�Ƃ��Ċg�����Ă��������
�@�����ł͎������s�����Ƃ��Ɏg�����f�[�^�̍쐬���@�ƌ��݂̔z�����@�̃A���S���Y���̐���������B�[�~�̔z�����ʂ̓[�~�̐l�C�̏�A�w���̐l�C�̏ɂ���ĕω����Ă����ƍl������B�Ⴆ�A�w�����o�����X�悭�[�~�Ɋ�]���o�����ׂĂ̐l����1��]�ɏ����ł���̂ɑ��A����P�̃[�~�ɐl�C���W������ƂقƂ�ǂ̊w���͑�P��]�ɏ����ł��Ȃ��A�Ƃ�������������ŗl�X�Ȑl�C�̃p�^�[�������A�f�[�^���쐬���悤�ƍl������f�[�^�ł͊w���̃[�~�ɑ��鏇�ʕt���A�[�~�̊w���ɑ��鏇�ʕt����2���������B�z�����@�ł͌��݂̔z�����@�̐��������顈��茋������Gale-Shapley�̃A���S���Y���͈��茋�����̐߂��Q�Ƃ��ė~�����
������w�ŊJ�݂����[�~�̐���15����B�o�����X�悭�w�����قȂ�[�~�Ɋ�]���o���قƂ�ǂ̐l����1��]�ɏ����ł���B���������ۂ͐l�C�̂���[�~�A�����ł͂Ȃ��[�~������A��]�҂������2�{�ȏ�̃[�~��A����1���̊�]�҂����Ȃ��[�~�Ȃǂ�����B�O�҂̃[�~�͊�]�҂̔����ȏオ��1��]�ɏ����ł��Ȃ��B���̂悤�Ƀ[�~�̐l�C�͑�1��]�ŕs���i�ƂȂ��Ă��܂��w���̐��ɊW���Ă���B�����Ŋw���̃[�~�ɑ��鏇�ʕt���̃f�[�^�쐬�ɓ������āA��茻���I�ȃf�[�^�ɂ���ׂɃ[�~�̐l�C��\�����ƍl�����
�@�A���S���Y�����܂��ɐ�������ƁA�e�[�~���Ƃɗ������������蓖�Ă�B���̗����̑傫�����Ƀ[�~����בւ���A��������ׂĂ̊w���ɑ��čs������̗����̑傫���[�~�̏����w���̃[�~�ɑ��鏇�ʂƂ������@���
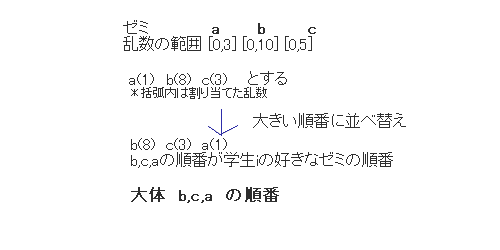
�@�K�͂̏����ȗ�ŏڂ����A���S���Y���������B�[�~a,b,c������Ƃ���B�[�~��b,c,a�̏��ԂŐl�C������B�����Ől�C�̂���[�~b�̗����̕���[0,10]�Ƃ��A���ɐl�C�̃[�~c�͗����̕���[0,5]�Ƃ��A���̃[�~a��[0,3]�Ǝw�肷��B�����Ċe�w�����Ƃɗ����������A�~���ɕ��בւ���Ƃ������@�ł��顂��̂悤�ɂ���[�~b�̗������傫���Ȃ�\�����傫���A�[�~a�̗������������Ȃ�\�����傫����i�}4.1�Q�Ɓj�@
�@�@�@�@�@�@�@�@�@�@�@�}4.1.�l�C�̂���[�~b�A�Ȃ��[�~a�̍쐬���@
|
�w�����ʕt���A���S���Y�� �����@�w���W���A�[�~�W���A�e�[�~�̗����͈̔́A�@ �o���@�w���̃[�~�ւ̏��ʕt�� step1 �e�w���ɑ��Ĉȉ��̍�Ƃ��J��Ԃ��B
step3 �@�L�[�̑傫�ȏ��Ԃɕ��בւ����[�~�̏������w���̑I�D���� |
������w�o�c���w�Ȃ�1�w�N�̊w�����͖�180���ł���B���̂��ׂĂ����ׂĂ̐搶���c������̂͂قڕs�\�ł���B����āA���ۂɂ̓[�~�̊w���ɑ��鏇�ʕt���͕s�\�ł���B�����ŁA�������̎�������āA�A���S���Y������}��B
�@�搶���w���ɑ��A����̊�Ƃ��čl������̂͐��сA���Ƒԓx�Ȃǂ��l������i������������Ȃ��������ł͍l�����Ȃ��j�B���т͑����̐��т�������Ɋւ��鐬�тŎQ�Ƃ���邾�낤�B�Ⴆ�AOR�[�~�̑I�l�̎��ɁA����w���̌o�c���v�̕���̐��т��ǂ��Ȃ��Ă�OR�̕���̐��т��悯����̊w����OR�[�~�ɍ��i���Ă��s���R�ł͂Ȃ��B���̂悤�Ɋw���ɑ��鏇�ʕt���̃f�[�^�����ہA��l�̊w���ɐl�C���W������̂ł͂Ȃ��A�[�~�̕��삲�ƂɍD�݂̊w�����U���悤�ɐݒ肵�����ƍl�����
�@�[�~�̊w���ɑ��鏇�ʕt���̃f�[�^�쐬�̊�{�I�ȃA���S���Y���͊w���̃[�~�ɑ��鏇�ʕt���ƕς��Ȃ�����̃A���S���Y�����K�͂̏����ȗ�Ő������顊w��1,2,...,10�ƕ���a,b������Ƃ��顕���a�̐��т̏����w��1,2,...,10�Ƃ��顕���b�̐��т̏����w��10,9,...,1�Ƃ���B���т���I�l����Ȃ番��a�̃[�~�͑��1,2,..,10�̏��ԁA����b�̃[�~�͑��10,9,...,1�̏��Ԃŏ��ʕt��������͂��ł���B�����ŗ������蓖�Ăɂ������ĕ���a�̗����̕����w��1��������傫�����蓖�ĂāA���̎��ɑ傫���̂��w��,2,..���������̂��w��10�̏��ԂƂ��A���蓖�Ă��l�̑傫�������[�~�̍D���ȏ��ԂƂ���Α��1,2,...10�̏��ԂƂȂ�B���l�ɕ���b�̃[�~��1�����������A10��������傫�������̕���^����悢�B�i�\4.1�Q�Ɓj
�@�@�@�@�@�@�@�@�@�@�@�@�\4.1�@�����͈̔͂������\
| �w�� 1,2...10 |
�w��11,12..,20 |
�E�E�E |
�w��90,91,...100 | |
| ����a | [0,10] | [0,9] | �E�E�E | [0,1] |
| ����b | [0,1] | [0,2] | �E�E�E | [0,10] |
����a�̃[�~i,j�͕���a�̍s�̗����̊��蓖�ĕ��Ŋw���ɒl�����蓖�Ă�
����a�̃[�~m,n�͕���b�̍s�̗����̊��蓖�ĕ��Ŋw���ɒl�����蓖�Ă�
�l�����蓖�Ă���͊w���̃[�~�ɑ��鏇�ʕt���Ɠ��l�ɍs��
�@���茋�����ł̕W���`�ɂ����Ă͏��ʕt���͑S�����ł��鎖�����肵�Ă���[4]�B�������A�[�~�̊w���ɑ��鏇�ʕt���͂��ׂĂ̊w�������ɕ��ׂ�悤�ȑS�����ł�������A����5�̂ǂ̊w�����������炢�̋C�����ŗ��ė~�����A�Ƃ������ɓ����ʂ������������R�ł���(�}4.2�Q�Ɓj�B���茋�������g���������ŏ��ʕt���ɓ����ʂ������ꍇ�Ƃ����̂�����A�����ł͂���𗘗p���顂��̒��ł������}�b�`���O�̒�`�Ŋg��������������ł܂��͎����}�b�`���O�̒�`��������A���̌�Ƀ[�~�̊w���ɑ��鏇�ʕt�����

�}4.2.�������т̊w���̓����_���ɏ��ʕt��
�@���ꂼ��̍D���ȏ��Ԃɂ����Ď����̃p�[�g�i�[�Ɠ����ʂ̑��肪�ǂ̂悤�ȃp�[�g�i�[�������͑S���C�ɂȂ�Ȃ��Ɖ��肵���ꍇ�A�ȉ��̂悤�ȃu���b�L���O�y�A�̒�`���ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@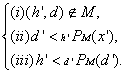
�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@�@�@�@(h',d')��M�ɂ�����u���b�L���O�y�A�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@���̃u���b�L���O�y�A�̑��݂��Ȃ��}�b�`���O�������}�b�`���O�ƌĂԁB
�@�����}�b�`���O����������@�͓����ʂ̗v�f������K���ɏ�����^���A���茋�����̕W���`�ɒ����AGale-Shapley�̃A���S���Y����K�p����悢�B���́h�K���h�ɂ͔C�Ӑ����܂܂�Ă���̂Œj���i�����j�ŗLj���}�b�`���O�͕������݂���
�@�����苭������̒�����}�b�`���O�A������}�b�`���O�Ƃ����̂����邪�A���������Ƃ��Ē�`����ƈ���}�b�`���O�����݂��邱�Ƃ��ۏ���Ȃ��B�����ł����ł͎����}�b�`���O���̗p���鎖�ɂ���
|
�[�~�̏��ʕt���A���S���Y�� �[�~�̏��ʕt���ɂ����Ď����}�b�`���O�����ׂɂ͂܂��A�[�~�̕�����Q�Ƃ��A�w�������̕���̐��т����5,4,3,2,1��5�̃O���[�v�ɕ�����A����ɂ��̒��œK���Ɋw���ɏ��ʕt�������Ă����悢��iNo11�Q�Ɓj �����@�w���W���A�A�[�~�W���A�[�~�̕���A�e�w���̗����͈̔� �o���@�[�~�̊w���ɑ��鏇�ʕt�� step0�@�e�[�~�ɂ��ď��ʂ������ĂȂ��i�����ݒ�j�B step1�@�e�[�~�ɂ��ă[�~�̕�����A�����ė����͈̔͂��w���Ɋ��蓖�Ă�B step2�@�e�[�~�ɂ��Ĉȉ��̍�Ƃ��J��Ԃ��B
step3�@�e�[�~�ɂ��Đ������Ԃ��w���ɑ���D���ȏ��ԁB |
���݂̔z�����@���A���S���Y��������ɓ������Ď��ۂƈقȂ�_�́A�w������ԍŏ��ɂ��ׂẴ[�~�ɑ��ď��ʕt�����ł��Ă���Ƃ������Ƃł���
���݂̔z�����@�A���S���Y�������@�w���̃[�~�ɑ���I�D�����A�[�~�̊w���ɑ���I�D���� �o���@�[�~�̔z�� step0 �ǂ̊w�����ǂ̃[�~�ɂ��z������Ă��Ȃ��B step1�@���ׂĂ̊w������������܂ŌJ��Ԃ��B���������Ȃ�step5�ɐi�ށB�@ step2 �w���͒���ɗ]�T�̂���[�~�ł����Ƃ��ŏ�ʂɂ���[�~�ɐ\�����ށB step3 �e�[�~�ɂ����Ĉȉ��̍�Ƃ��s���B
step4�@step1�ɖ߂�B step5 �I�����ꂽ�[�~���A���̊w������������[�~�B �@ |
���茋������Gale-Shapley�̃A���S���Y���ƁA�O�͂ŃA���S���Y�����������݂̔z�����@�̃v���O�������쐬���A�f�[�^�����̃v���O�����ɂ����Ď������s�����B20�ʂ�̐l�C�̃p�^�[�����쐬���A1�ɂ�1000��̔z�����s�����Ƃ���V�~�����[�V�����̌��ʂ������A�l�@�ɓ���B�Ȃ������ł͊ȒP�̂��߃[�~�̐���15�A�w����150�l�A�����10�l�A�[�~�̕����3�Ƃ��Ă���B
�@�@�l�C�̂���[�~����ɏW������Ƒ�1��]�ɏ����ł��Ȃ��w���͑����A���ɐl�C�̂���[�~�A�����łȂ��[�~�̍������܂�Ȃ��Ƃ��͑�̑�1��]�ɏ����ł���B�����Ńf�[�^�쐬�ɂ�����A�[�~�̐l�C�ɂ��Đl�C�̏W�������p�^�[���Ɛl�C�̕��U�����p�^�[�������A�������s�����ƍl�����B�l�C�̕��U�̕��@�͊w���̏W����3�̃O���[�v�ɕ����A�i�l�C�W���i���j�̓O���[�v�����Ȃ������j���ꂼ��A3�̃p�^�[���ɂ��������ď��ʕt�����s���悤�ɂ����i�\5.1�Q�Ɓj�B
�@�l�C�̏W�������p�^�[���ƕ��U�����p�^�[���ɂ��Ă��ꂼ�ꋭ���l�C�W���i���U�j�A�ア�l�C�W���i���U�j��2�ʂ�̃f�[�^�����������B�܂��A�l�C�̂���[�~�����łȂ��[�~���쐬���Ȃ����S�Ƀ����_���̃f�[�^�̍쐬���v���O�����ɂ������
�@�\5.1�͂��̐l�C�̃p�^�[����������Ⴆ�ΐl�C���U�i���j�̕\�̂��Ƃł̃f�[�^�쐬���@�ɂ��āA�O���[�v1�Ń[�~�����ʕt������w���̓[�~1,...,5�ɍł������������A�[�~6,...,10�ɂ͏����������Ȃ��A�Ƃ����悤�ȏ��ʕt�����s���悤�ɂ��顏W���i���j�̎��͂��ׂĂ̊w�����[�~1,...,5�ɍł������������A�[�~11,...,15�ɂ͏����������Ȃ��Ƃ������ʕt�����s���悤�ɂȂ顂��̂悤�ɐl�C�̏W���x��ς��ăf�[�^���쐬�����
�\5.1.�[�~�̐l�C�̏W�����4�ɕ����ăf�[�^�쐬
�l�C���U�i���j
| �@ | �[�~1,..,.5 | �[�~6,...,10 | �[�~11,...,15 |
| �O���[�v1 | �� | �~ | �� |
| �O���[�v2 | �� | �� | �~ |
| �O���[�v3 | �~ | �� | �� |
�l�C���U�i��j
| �@ | �[�~1,..,.5 | �[�~6,...,10 | �[�~11,...,15 |
| �O���[�v1 | �� | �� | �~ |
| �O���[�v2 | �� | �� | �� |
| �O���[�v3 | �� | �� | �� |
�l�C�W���i��j
| �@ | �[�~1,..,.5 | �[�~6,...,10 | �[�~11,...,15 |
| �O���[�v1 | �� | �� | �� |
| �O���[�v2 | �� | �� | �� |
| �O���[�v3 | �� | �� | �� |
�l�C�W���i���j
| �@ | �[�~1,..,.5 | �[�~6,...,10 | �[�~11,...,15 |
| �O���[�v1 | �� | �� | �~ |
���F�l�C������[�~
���F�l�C�����ʂ̃[�~
�~�F�l�C���Ȃ��[�~
�l�C�t���ɓ������ă[�~�̊w���ɑ���l�C�t�������l�ɍs������Ⴆ�ΐl�C���U�i���j�̕���1�ɂ����Ċw���ԍ�1,...,50�Ԃ̊w���͍ł��������ė~�����A�w���ԍ�51,...,100�Ԃ̊w���͏������ė~�����Ȃ��Ƃ������ł��顕\5.2�̂悤�ɕ����3�ɕ����A���ꂼ��̕���̊w���ɑ���l�C�t���̃p�^�[����ς��Đl�C�̏W���x��ω��������B
�\5.2�w���̐l�C�̏W�����4�ɕ����ăf�[�^�쐬
�l�C���U�i���j
| �@ | �w��1,..,.50 | �w��51,...,100 | �w��101,...,150 |
| ����1 | �� | �~ | �� |
| ����2 | �� | �� | �~ |
| ����3 | �~ | �� | �� |
�l�C���U�i��j
| �@ | �w��1,..,.50 | �w��51,...,100 | �w��101,...,150 |
| ����1 | �� | �� | �~ |
| ����2 | �� | �� | �� |
| ����3 | �� | �� | �� |
�l�C�W���i��j
| �@ | �w��1,..,.50 | �w��51,...,100 | �w��101,...,150 |
| ����1 | �� | �� | �� |
| ����2 | �� | �� | �� |
| ����3 | �� | �� | �� |
�l�C�W���i���j
| �@ | �w��1,..,.50 | �w��51,...,100 | �w��101,...,150 |
| ����1 | �� | �� | �~ |
���F�l�C������w��
���F�l�C�����ʂ̊w��
�~�F�l�C���Ȃ��w��
�@�O�͂�5.2��5.3�ł��ꂼ��쐬�����[�~�̐l�C�A�w���̐l�C���g���ăV�~�����[�V�������s���B�w���̐l�C���W���i���j�̎��A�[�~�̐l�C�Ƃ̑g�����̐��́A�[�~�̐l�C�W���i���j�A�W���i��j�A���U�i��j�A���U�i���j�A�����_����5�ʂ�ł��顓��l�Ɋw���̐l�C���W���i��j�̎���5�ʂ肠��B�܂�A�w���̐l�C�t���̃p�^�[��4��ނƁA�[�~�̐l�C�t���̃p�^�[��5��ނ��悶�����A20�ʂ�̐l�C�̃p�^�[��������B1�̑g�����i�Ⴆ�Ίw���̐l�C���W���i���j�ƃ[�~�̐l�C�����U�i��j�̑g�����j�ɂ��A1000��̔z�����s�����Ƃ���V�~�����[�V�������s���A�w���͉��Ԗڂɏ����������[�~�ɏ��������̂��̓��v���Ƃ����B
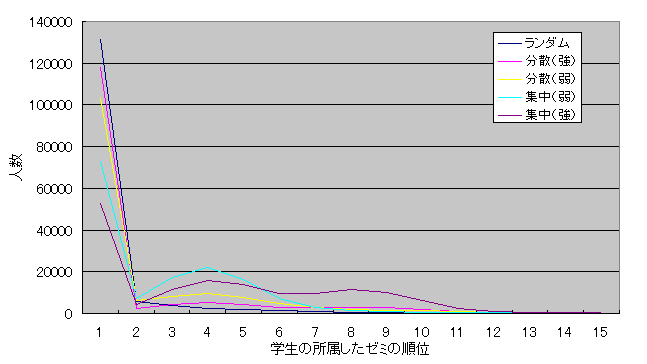
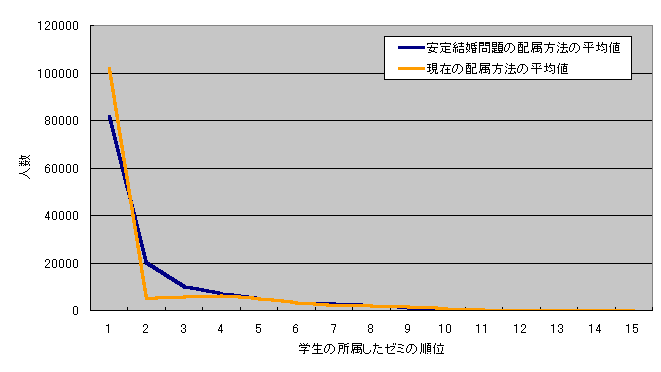
�@�}6.1�͌��݂̔z�����@�̃V�~�����[�V�����̌��ʂŁA20�ʂ�̑g�����̌��ʂ̕��ϒl���O���t�ŕ\�������̂ł���B�܂��}6.2�͈��茋������Gale-Shapley�̔z�����@�̃V�~�����[�V�����̌��ʂł���B���݂̔z�����@�A���茋�����̔z�����@�̂ǂ���̔z�����@�̂ǂ̐l�C�̏W���p�^�[�����A��P��]�ɏ����ł���w���̐����ł������A��15��]�Ɍ������ɂ��������Ă���Ɛl�����������Ă����E������̃O���t�ł��顂܂��ǂ���̌��ʂ��A����[�~�ɐl�C���W�����Ă���Ƒ�P��]�ɏ����ł���w���̐l���͏��Ȃ��A�l�C�ɂ��������Ƒ�P��]�ɏ����ł���w���������Ȃ��Ă��顓��Ɍ��݂̔z�����@�ɂ����ă[�~�̐l�C�������_���̎��A��P��]�ɏ����ł���w�����قƂ�ǂł��鎖���킩�顔��Ɉ��茋�����ɂ����ă[�~�̐l�C���W���i���j�̎��A��P��]�ɏ����ł���w����20%�ɖ����Ȃ��B�i���v��150000�l�j
�@�@�@�@�@�@�@ �}6.1
���݂̔z�����@�̃[�~�z���V�~�����[�V����
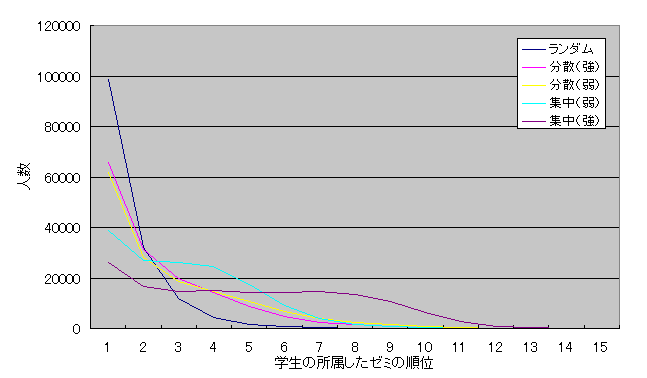
�@�@�@�@�@�@�@�@�}6.2�@���茋������Gale-Shapley�̃[�~�z���V�~�����[�V����
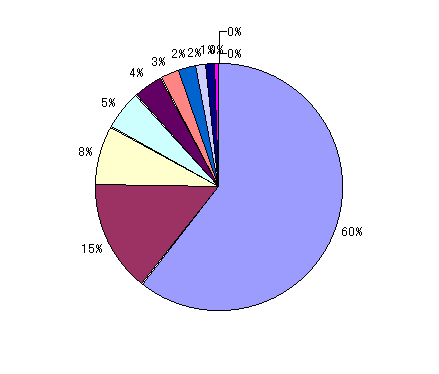
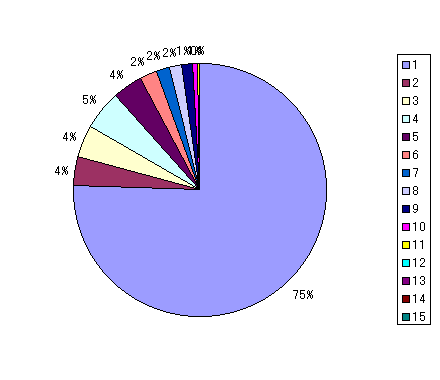
�@�}6.3�͐}6.1�̌��݂̔z�����@�̌��ʂ̕��ρA�}6.2�̈��茋�����̔z�����@�̌��ʂ̕��ϒl���O���t�ɂ������̂ł��顈��茋�����������݂̔z�����@�̕�����P��]�ɏ����ł���l�����������������顐}6.4�Ɛ}6.5�͐}6.3�̊������~�O���t�Ŏ��������̂����A�}6.5�̌��݂̔z�����@�ł͑�P��]�ɏ����ł���l����60%���z����}6.4�͈��茋�����̔z�����@�ŁA��P��]�ɏ����ł���w����30%�ゾ�����B
�@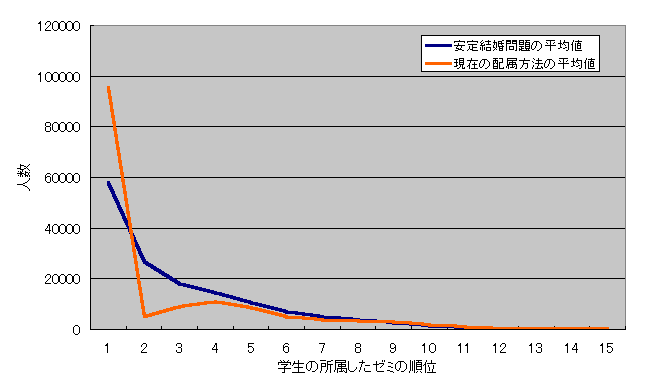
�}6.3 �}6.2�̈��茋�����̌��ʁA�}6.1�̌��݂̔z�����@�̌��ʂ̕��ς̔�r
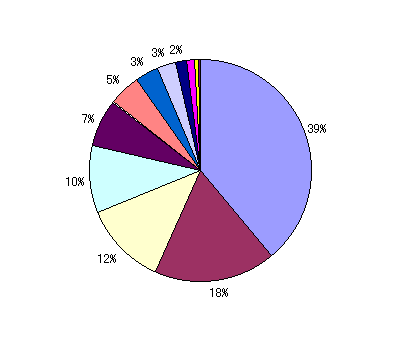
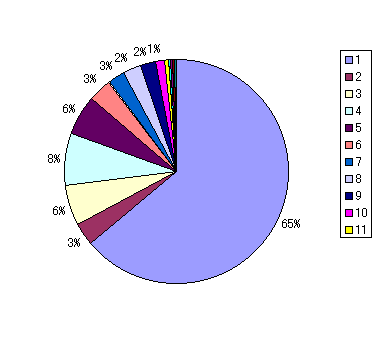
�@�@�@�@�@�@�@�}6.4�@���茋�����ł̔z����]���ʂ̊����@�@�@�@�@�@�@�@�@�@�@�@�@�@�}6.5�@���݂̔z���ł̔z����]���ʂ̊���
�O�߂Ɣ��ɁA�[�~���猩�ď��������w���͂ǂ̂��炢�D�܂����̂��Ƃ������v���Ƃ����B�[�~���w���ɑ��A1�Ԃ���150�Ԃ܂ŏ��ʕt�����s���Ă����Ƃ��āA1�Ԃ���30�Ԃ܂ŁA 31�Ԃ���60�Ԃ܂ŁA 61�Ԃ���90�Ԃ܂ŁA91�Ԃ���120�Ԃ܂� 121�Ԃ���150�Ԃ܂ł�5�̃����N�ɕ����ē��v���Ƃ�����}6.6�͌��݂̔z�����@�ōs�����ꍇ�A�}6.7�͈��茋������Gale-Shapley�̔z�����@�ōs�����ꍇ�̌��ʂł���B�ǂ���̔z�����@���[�~�̐l�C�ɎU��肪����ꍇ�̂ق����ł����������N�̊w���̐l�����ł������A�l�C���W�������ꍇ���ł����Ȃ��Ȃ��Ă��顐}6.8�͈��茋�����̔z�����@�ƌ��݂̔z�����@�̂��ׂẴV�~�����[�V�����̌��ʂ̕��ϒl���O���t�ŕ\�������̂ł���B�ǂ���̔z�����@���E������ŁA���l�����Ȃ莗�Ă��顐}6.9�͐}6.8�̈��茋�����̐��l�������Ŏ��������́A�}6.10�͌��݂̔z�����@�̐��l�������Ŏ��������̂ł���90%�ȏ�̊w���͂��̃[�~��60�Ԉȓ��ɍD�܂��������킩��

�@�@�@�@�@�@�@�@�@�}6.6�@���݂̔z�����@�̃[�~�z���V�~�����[�V����
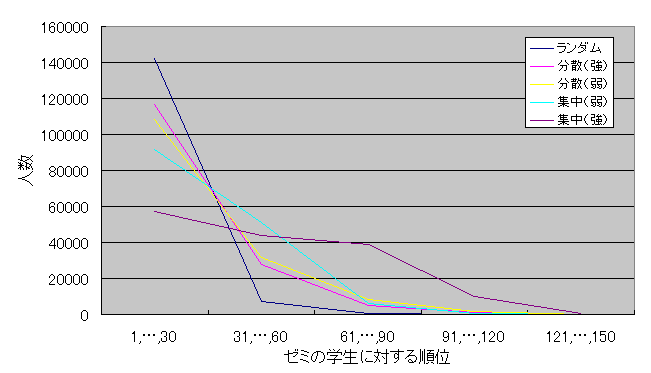
�}6.7�@���茋������Gale-Shapley�A���S���Y���̃[�~�z���V�~�����[�V����
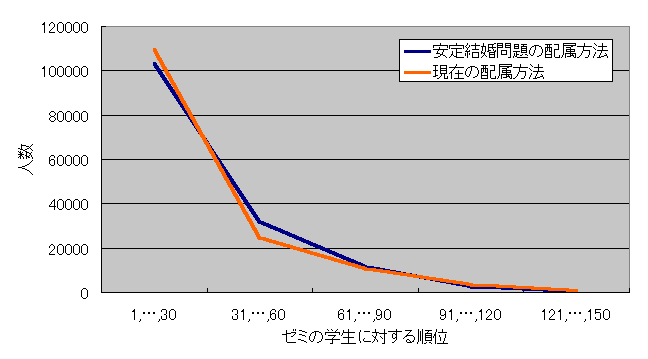
�@�@�@�@�@�@�@�@�@�@�@�}6.8�@�}6.6�̌��݂̔z�����@�̕��ϒl�Ɛ}6.7�̈��茋�����̕��ϒl�̃O���t
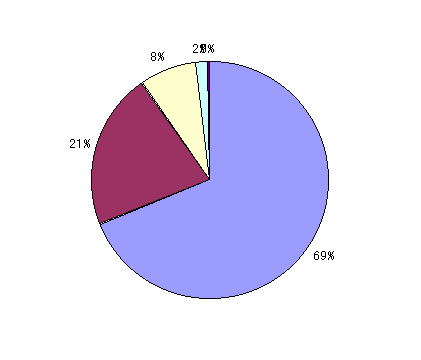
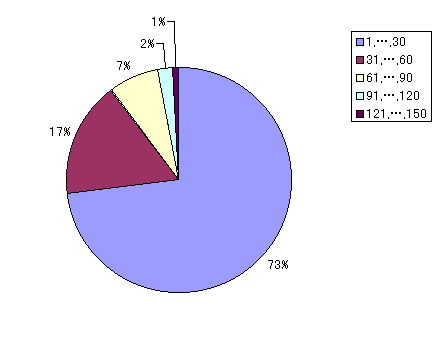
�@�@�@�@�@�@�@�@�}6.9�@���茋�����ł̃[�~�̊w���ɑ��郉���N�̊����@�@�@�@�@�@�@�}6.10�@���݂̔z�����@�ł̃[�~�̊w���ɑ��郉���N�̊���
6.1�ł͊w�������[�~���ƃ[�~�̒�������悶�����ɓ�������������̂��߁A���ׂẴ[�~���[�~�̒���s�b�^���Ɋw���������A�ł������������Ȃ��[�~�ɏ�������w�������݂��Ă��܂����Ƃ��������l�����顂����ł��̐߂ł͒���̐��𑝂₵�������s�����i�}6.11�Q�Ɓj�����ɂ��[�~�ɂ���Ċw���̏�������l�����ω�����B�܂��A����𑝂₷���ɂ���1��]�ɏ����ł���w���̐l���̊������������鎖���\���ł��顂��̎������s���ɓ������ă[�~���Ƀ[�~�̒�����悶�����𑍗e�ʂƒ�`����B������w�ł͂��̑��e�ʂ��w�����̉��{���炢�Ȃ̂��ׂ��������w�ł͑��1�w�N��180���ł���B�[�~����15�A�����14�l�ł���̂ő��e�ʂ�210�ł��顂��̂��Ƃ���A���e�ʂ͊w�����̑��1����2���������炢�ł��鎖���킩�顂��̎������瑍�e�ʂ��w����1�������Ƃ����ꍇ�ƁA2�������Ƃ����ꍇ�̎������s����������̕��@�͊w�����Ƒ��e�ʂ����������ɍs�������Ɠ����悤��20�ʂ�̑g�����A1�̑g�����ɂ�1000��̔z�����s���Ƃ����V�~�����[�V�����ł���
�}6.10�@�[�~�̒���𑝂₵���ꍇ�A�w��a,b,...,k,l��z���������A�\�z�ł���z���̕ω�
�����ł͑��e�ʂ��w����1�����Ƃ������A�w���͉��ԖڂɍD�܂����[�~�ɏ����ł����̂��Ƃ������v���ʂ�������}6.21��20�ʂ�̃p�^�[���̕��ϒl���O���t�ɂ�����}6.22�͈��茋�����̔z�����@�A�}6.22�͌��݂̔z�����@�ɂ�����w�������������[�~�̏��ʂ̊����ł��顂ǂ���̔z�����@�����e�ʂƊw��������������������1��]�ɏ����ł���w����������������Ɉ��茋�����̔z�����@��30%�ォ��60%�ւƑ啝�ɑ�1��]�ɏ����ł���w��������������Ȃ��A���݂̔z�����@�ł̍ň����ʂ�15�ʁA���茋�����ł̍ň����ʂ�13�ʂ������
�}6.21�@���e�ʂ��w����1�������̎��̕��ϒl
�}6.22�@���茋�����̔z�����@�ɂ�����w���̏��������[�~�̏��ʂ̊����@�@�@�@�@�@�}6.23�@���݂̔z�����@�ɂ�����w���̏��������[�~�̏��ʂ̊���
�@
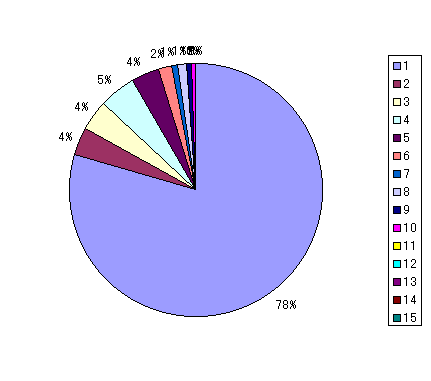
�@�����ł͑��e�ʂ��w����2�����Ƃ������A�w���͉��ԖڂɍD�܂����[�~�ɏ����ł����̂��Ƃ������v���ʂ�������}6.24��20�ʂ�̃p�^�[���̕��ϒl���O���t�ɂ�����}6.25�͈��茋�����̔z�����@�A�}6.26�͌��݂̔z�����@�ɂ�����w�������������[�~�̏��ʂ̊����ł��顂�͂葍�e�ʂ�1�����̎�������1��]�ɏ����ł���w����������������茋�����͊w���̃[�~�ɑ����]�����ł����4��]���w���̍ň����ʂƂ������ʂ��o�����i�t�^�Q�Ɓj�B���݂̔z�����@�͑�1��]�ɏ����ł���w���̊�����78%�Ƃ��Ȃ荂�����l�ł��顂܂����݂̔z�����@�ł̍ň����ʂ�12�ʁi1/120000�̊m���j���茋������12�ʁi1/120000�̊m���j�������B
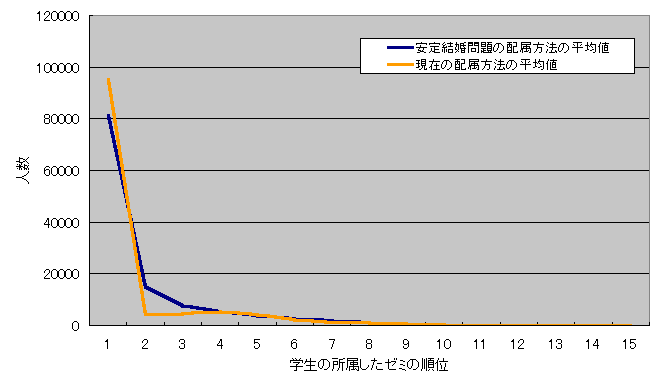
�}6.24�@���e�ʂ��w����1�������̎��̕��ϒl

�}6.25�@���茋�����̔z�����@�ɂ�����w���̏��������[�~�̏��ʂ̊����@�@�@�@�@�@�}6.26�@���݂̔z�����@�ɂ�����w���̏��������[�~�̏��ʂ̊���
�@40000��̃V�~�����[�V�����̌��ʂ���A���݂̔z�����@�͊w������1��]�ɏ����ł��銄�����ł������B���̌�͑�2��]�A��3��]�Ɛl���������Ă����̂ł͂Ȃ��A�ꍇ�ɂ���Ă͑�3��]������������A��4��]�����������肷��B�[�~���猩���w���̏����͊w�����I��ł��̒�����D�܂����w����I��ł���Ƃ����z�����@�̊��ɂ͍D�܂����w�����قƂ�ǂƂ������ʂɂȂ����
�@���茋������Gale-Shapley�̃A���S���Y���ł̔z�����@�����݂̔z�����@�Ɠ��l�ɑ�1��]�ɏ����ł��銄�����ł������A���̌�͑�̑�2��]�A��3��]�Ə��Ȃ��Ȃ��Ă����B�[�~���猩���w���̏��A���݂̔z�����@�Ɠ��l�ɍD�܂����w�����قƂ�ǂƂ������ʂɂȂ����
�@�܂��A���e�ʂ�������Α�1��]�ɏ����ł���w�����������A����ɒႢ���ʂɑ�����w���̊��������������B���茋�����ɂ����āA�w���̑��e�ʂ��w����1�������Ƃ�����60%�A2����������68%�Ɗw�����Ƒ��e�ʂ����������Ɣ�ׁA�啝�ɑ������������������ɁA���݂̔z�����@�ɂ����ẮA��1��]�ɏ����ł���w���̑����̊����͑��e�ʂ��w����1�����̎�70%�A2�����̎�78%�Ɣ��ɍ����Ȃ��Ă���B�@��2��]�͈��茋�����̕��������B��̈��茋�����̑�1��]�Ƒ�2��]�̊����̘a�����݂̔z�����@�̑�1��]�̊����ɓ������Ȃ��Ă��顂���ȍ~�Ɋւ��Ċώ@���Ă݂�ƁA�}6.21�A�}6.24��������Ă킩��悤�ɂǂ���̔z�����@�������悤�Ȋ����ŏ������Ă���B
�@�܂��}6.9�A6.10�̃O���t����A�[�~�ɂƂ��Ă͂ǂ���̔z�����@�������悤�Ȍ��ʂɂȂ�A�ǂ���̔z�����@�ł��[�~�͂��܂�Ȃ��A�Ƃ�������������������ǂ���̔z�����@�����������w���́A�[�~��60�Ԉȓ��ɏ��ʕt�������w����90%���߂�
�@�ȏ�̎����猻�݂̔z�����@�̕��͑�1��]�ɏ����ł���w���������A����ȍ~�̊w���̏����������ʂɂ��Ă����茋�����ɗ��Ȃ����Ƃ������A������w�̃[�~�̔z���͈��茋�����̔z�����@�������݂̔z�����@�Ŕz�������ق����ǂ��Ƃ��������킩�����
�@���茋�����̔z�����@�͊w���ŗǂ̔z�����@�ōs������܂�A���茋�����ł͊w���ɂƂ��Ă���ȏ�ǂ��z���͏o���Ȃ����Ƀ[�~�̏��������w���ɑ��郉���N�͑��̈���Ȕz�����s���悭�Ȃ��Ă������낤�B�������A�w���ŗǂ��ł��D�܂����z���̊w���̏������鏇�ʂ͈����Ȃ��Ă����B
�@���茋�����͈���𐧖�Ƃ���Ƃ��ɂ��A�w���ŗǂƂ����ǃ[�~�ɂ��s���̂Ȃ��悤�ȂƂ����z�����s���Ă��܂��w���ɂƂ��Ă͗ǂ��Ȃ����ʂɎ������Ƃ������Ƃ��l�����顖{���w���̈ӌ����ŗD��ɂ��ׂ��[�~�z���ɁA�[�~�̈ӌ����w���ƑΓ��Ɏ���Ă��܂����茋�����̓[�~�z���Ɍ����Ă��Ȃ������킩�����
����͔z�����̃A�v���[�`�Ƃ��Ĉ��茋�������̗p��������̌��ʁA���茋�������g�������z���͕�����w�̃[�~�z���ɂ͓K���Ă��Ȃ������킩�����B�m���Ɍ��݂̔z�����@�͈��茋�����̔z�����@�����ǂ��z�����Ƃ������ʂ�����ꂽ���A���͌��݂̔z�����@���ł��ǂ��z���ł���Ƃ͍l���Ă��Ȃ��
�@������3�͂ŏЉ�����`�v��ŃA�v���[�`�����悤�ƍl���Ă��顐��`�v��ł̃[�~�z���͎��ۂɍ̗p���Ă����w������Ƃ�����������[6]�A�ǂ����ʂ����҂ł���B�ł͕�����w�ł͂ǂ̂悤�ɂ͂ǂ̂悤�ɃA�v���[�`����悢�����l����B�܂�������w�ł͌��݂̔z�����@�ɂ�����,�A�[�~�̋������[�~�z���Ɋւ���Ă���Ƃ�����������w�������łȂ��[�~����������悤�Ȕz�������Ȃ��Ă͂Ȃ�Ȃ���z���Ă��Ă���ɓ������Ċw���̃[�~�ɏ����������̖����x�����ł͂Ȃ��A�[�~�̊w���ɑ��閞���x���Q�Ƃ���Ƃ������Ƃł���B���̎��A���ʂ��x�Ƃ��ĖړI�����ŏ����Ƃ���Ηǂ��i�}8.1�Q�Ɓj�B
�@���̎��A�\8.1�A8.2�̂悤�ɖ����x��ݒ肷��Γ����ʂ��\���ł���B�����ł��������ʂƂ͊w���i�[�~�j���ǂ�����������炢�̋C�����ŕ����̃[�~�i�w���j�ɏ����������i���ė~�����j�Ƃ������Ƃł��顗Ⴆ�Ε\8.1�̓[�~a�͊w��1��2�͓������炢�ǂ���ɂ����ė~�������������Ă��顐}8.1�͕\8.1�A8.2����莮���������̂ł���B
�\8.1�@�@�����ʂ��������[�~a,b,c�̊w��1,2,...,4�ɑ��鏇�ʕt��
| �@ | �w��1 | �w��2 | �w��3 | �w��4 |
| �[�~a | 1 | 1 | 3 | 3 |
| �[�~b | 2 | 1 | 4 | 2 |
| �[�~c | 3 | 1 | 2 | 4 |
�@
�\8.2�@�@�����ʂ��������w��1,2,...,4�̃[�~a,b,c�ɑ��鏇�ʕt��
| �@ | �[�~a | �[�~b | �[�~c |
| �w��1 | 1 | 2 | 3 |
| �w��2 | 1 | 3 | 1 |
| �w��3 | 2 | 1 | 3 |
| �w��4 | 3 | 1 | 1 |
�@
�@min. //�����x���ŏ��ɂ���i��]���ʂ��x�Ƃ��邽�߁j
�@�@�@�@�@//�[�~�̊w���ɑ��鏇�ʕt��
1X11+1X12+3X13+3X14
+2X21+1X22+4X23+2X24
+3X31+1X32+2X33+4X34
�@�@�@�@//�w���̃[�~�ɑ��鏇�ʕt��
+1X11+2X21+3X31
+1X12+3X22+1X32
+2X13+1X23+3X33
+3X14+1X24+1X34
�@s.t. //����̐���
X11+X12+X13+X14<=�[�~�̒��
�@�@ �@ X21+X22+X23+X24<=�[�~�̒��
X31+X32+X33+X34<=�[�~�̒��
//�w���͕K���ЂƂ̃[�~�ɏ������Ȃ��Ă͂Ȃ�Ȃ��Ƃ�������
�@�@�@�@X11+X21+X31=1
X12+X22+X32=1
X13+X23+X33=1
X14+X24+X34=1
�}8.1 �\8.1,8.2����莮��
�@�������A���̃f�[�^���쐬����ׂɂ͌��݂̔z�����@����茋�����Ŏg�����f�[�^�Ƃ͈Ⴄ�f�[�^���g��Ȃ��Ă͂Ȃ�Ȃ���Ȃ��Ȃ�A���茋�����͊w���̃[�~�ɑ��鏇�ʕt���ɂ����Ă͓����ʂ̃[�~���m�[�~�̊w���ɑ��鏇�ʕt���͓����ʂ̊w�����m��K���ɕ��ׂ邾���ŁA����ȉ�������ꂽ�i�����Œ�`���Ă���ׁj����ł���B�܂茻�ݍ쐬���Ă���w���̃[�~�ɑ���i�[�~�̊w���ɑ���j�f�[�^�쐬�v���O�����̓[�~a�͊w��1�A2���1��]�Ƃ��Ȃ��Ă��A�w��1��2�͑�1��]�����A�w��2�����ɑ�2��]�Ƃ��悤�Ƃ������ɂ��ăf�[�^���쐬���Ă���B���̂悤�ɂ��Ă�����ȉ������߂�̂ɖ��͂Ȃ�����̂��Ƃ�����`�v��ł̃A�v���[�`�ƌ��݂̔z�����@�̔�r�ׂ̈ɂ̓f�[�^�쐬�̉��ǂ��K�v�ł��顂���ɐ��`�v��A�v���P�[�V�������g�����V�~�����[�V�����̕��@���w�Ȃ���Ȃ�Ȃ����낤�
�@���̂悤�ɂ��ׂ����͂킩���Ă���B��������������݂̔z�����@�Ɣ�r�ł����Ȃ炨�����낢�̂ł͂Ȃ����
�{�_���͎������ł͊��������鎖�͂ł��܂���ł����B����̃[�~�i�[���ł�4�N���̃[�~�̃����o�[����A�����ăe�[�}���\��A���Ԕ��\��ł�3�N���̃[�~�̃����o�[���瑽���̎w�E�A�A�h�o�C�X�����������܂����B�܂��A�x�c�搶�ɂ͕s���S�ȃv���O���������Ă��������A�ڍׂɂ킽���ċ����Ă��������܂������������̃A�h�o�C�X�A�q���g���玑���̏Љ�܂Ŏw�������̍��{�搶�ɂ͖{���ɂ����b�ɂȂ�܂���������Ɏӈӂ�\���܂�����肪�Ƃ��������܂����
[1] �R�{�F�k�E�v�ۊ��Y�G����Z�[���X�}�����ւ̏��ҁG���q���X�G1997
[2] �R�{�F�k�G�o�c�H�w�T�_�Ghttp://www.sk.tsukuba.ac.jp/~yamamoto/ �G1999
[3] ���{�@�r�j�G���W�����G2000
[4] ��@�r�G�GC�ɂ��A���S���Y���ƃf�[�^�\���G���W���G1999
[5] �|�c�@�m�E��с@�r���E�l�c�@���i�GC����̊�b�G���{���H�o�ʼn��G1993
[6] ����@�_�G��������@����@�L�����p�X��OR�G���q���X�G1992
�@�ȉ�2�̃v���O�����͊w���̃[�~�ɑ��鏇�ʕt���A�[�~�̊w���Ƀ^���鏇�ʕt���A���݂̔z���A���S���Y���A���茋�����A���S���Y����4�̃v���O�����̑g��������Ȃ��Ă���B
�@���݂̔z�����@�̃v���O�����͊w���̃[�~�ɑ��鏇�ʕt���A�[�~�̊w���Ƀ^���鏇�ʕt���A���݂̔z���A���S���Y���̃v���O�����̑g�����A���茋�����̔z�����@�̃v���O�����͊w���̃[�~�ɑ��鏇�ʕt���A�[�~�̊w���ɑ��鏇�ʕt���A���茋�����̃A���S���Y���̑g�����ō쐬������ǂ���̃v���O�������A���e�ʂ��w������葽���^�C�v�ō쐬�������̂�������w���̃[�~�ɑ��鏇�ʕt���ƃ[�~�̊w���ɑ��鏇�ʕt���͕\5.1�A5.2�̒��̂ǂꂩ�̃p�^�[���ɂ��������Ă���B