第一章 はじめに
渋滞を避け少しでも目的地に着きたいと思い、私は料金を払って有料(高速)道路を利用してみることがあります。しかし同乗している友人の中にはお金を払うくらいなら少しくらい時間がかかってもなるべく安い経路にしようという人もいます。
もし、このような道路構造、目的地までの距離、所要時間や利用料金などに対する価値観の違いで経路が選ばれそのことによりこの道はいつも混むという現象が生まれるんだとしたら、人々の価値観から道路交通を選ぶ指標のようなものが見つけられるのではないかと思いました。
交通サービスや時間というのは形として残るものではないのでそのものの値段が妥当であるかははっきりとしていません。しかし決められて値段を払って利用しています。
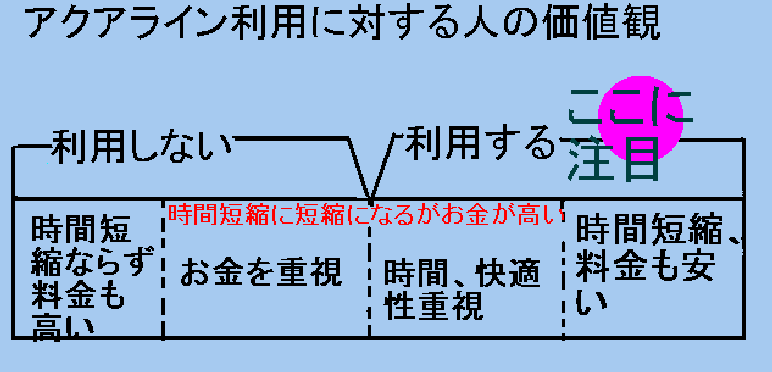
有料(高速)道路を利用する人は時間と、交通サービスを料金で買う行為をしているのではないかと見ることができます。
有料(高速)道路を利用しない人は、その決められた値段が妥当ではないと思うからから利用しないのでしょうか。経路選択を左右する道路交通を心理的にではなく、所要時間、利用料金といった面から交通サービス利用の選択の指標について考え、提案したいと思います。
そこでモデルの対象をベイエリア周辺の道路交通の中でアクアラインを利用する人、しない人の境目となる価値観の境目を数字として表わせたらとおもいこの研究を始めました。
第二章 ベイエリアについて
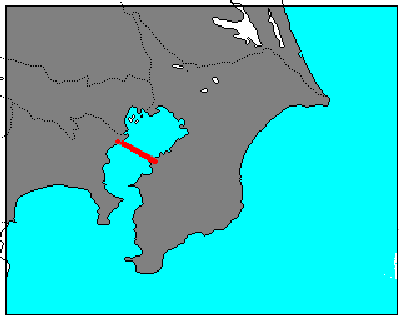
交通量の変化
第一エリア・・・横須賀、逗子、朝比奈、港南台、日野、別所、狩場、永田、花之木
第二エリア・・・石川町、山下町、新山下
第三エリア・・・大黒ふ頭、東扇島、浮島
第四エリア・・・湾岸環八、空港中央
第五エリア・・・大井南、大井JCT、13号地
第六エリア・・・有明JCT
第七エリア・・・新木場
第八エリア・・・葛西JCT
第九エリア・・・浦安、千鳥町、湾岸市川、湾岸習志野、湾岸千葉、宮野木、市原、姉崎袖ヶ浦
第十エリア・・・木更津北、木更津南、君津、浅間山、竹岡、金谷、保田、岩井勝山、富浦
| 第一 | 第二 | 第三 | 第四 | 第五 | 第六 | 第七 | 第八 | 第九 | 第十 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 第一エリア | 89 | 2558 | 1927 | 1628 | 547 | 339 | 932 | 559 | 2226 | 543 |
| 第二エリア | 2699 | 7419 | 4846 | 4220 | 1463 | 423 | 1918 | 1092 | 2070 | 1012 |
| 第三エリア | 2347 | 4863 | 449 | 1527 | 838 | 728 | 2797 | 1538 | 2878 | 1538 |
| 第四エリア | 1638 | 3086 | 1062 | 610 | 326 | 1595 | 5418 | 3479 | 5774 | 2309 |
| 第五エリア | 532 | 1081 | 705 | 234 | 66 | 739 | 2861 | 1744 | 3611 | 987 |
| 第六エリア | 297 | 616 | 515 | 1538 | 605 | 329 | 1479 | 953 | 2856 | 1163 |
| 第七エリア | 1060 | 1774 | 2300 | 4247 | 2636 | 2479 | 276 | 2279 | 10631 | 2741 |
| 第八エリア | 634 | 1141 | 1621 | 3508 | 1592 | 1153 | 2075 | 189 | 1249 | 895 |
| 第九エリア | 1551 | 2043 | 2923 | 5311 | 3117 | 2765 | 9139 | 1162 | 2226 | 543 |
| 第十エリア | 766 | 1129 | 1472 | 2130 | 980 | 1115 | 2935 | 1262 | 731 | 75 |
| 第一 | 第二 | 第三 | 第四 | 第五 | 第六 | 第七 | 第八 | 第九 | 第十 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 第一エリア | 92 | 2660 | 2004 | 1693 | 570 | 352 | 970 | 580 | 1830 | 553 |
| 第二エリア | 2806 | 7715 | 5040 | 4388 | 1520 | 439 | 1994 | 1135 | 1806 | 960 |
| 第三エリア | 2440 | 5057 | 466 | 1588 | 871 | 757 | 2908 | 1609 | 2452 | 1380 |
| 第四エリア | 1703 | 3309 | 1104 | 634 | 339 | 1660 | 5634 | 3618 | 4779 | 1997 |
| 第五エリア | 553 | 1124 | 733 | 243 | 68 | 768 | 2975 | 1814 | 3038 | 939 |
| 第六エリア | 308 | 640 | 535 | 1599 | 629 | 342 | 1538 | 991 | 2434 | 1080 |
| 第七エリア | 1102 | 1844 | 2392 | 4416 | 2741 | 2370 | 287 | 2370 | 10005 | 2342 |
| 第八エリア | 659 | 1186 | 1686 | 3648 | 1655 | 1200 | 2158 | 196 | 1149 | 866 |
| 第九エリア | 1390 | 1784 | 2488 | 4399 | 2643 | 2362 | 8811 | 1079 | 1930 | 534 |
| 第十エリア | 762 | 1053 | 1327 | 1854 | 934 | 1042 | 2498 | 1159 | 760 | 78 |
第三章 人の流れの変化
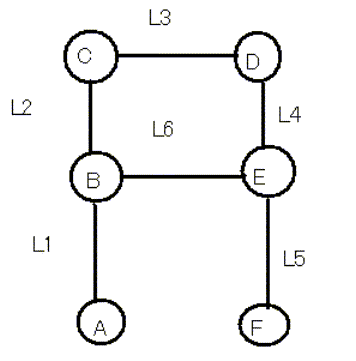 ①ベイエリア周辺の道路交通を単純に考えて6つの点A,B,C,D,E,Fに分けてみる。
①ベイエリア周辺の道路交通を単純に考えて6つの点A,B,C,D,E,Fに分けてみる。
②各点から各点へ移動するのにかかる距離や時間、道路使用料金を枝と設定する。その枝の長さをそれそれ、L1={A,B}、L2={B,C}、L3={C,D}、L4={D,E}、L5={E,F}とする。例えば、AからDへ移動するにはL1+L2+L3の枝の長さ分かかることになります。
④そこえ新たにBとEの点を結ぶ道ができてその枝をL6={B,E}とする。点BとEを結ぶ道ができたことによってAからDへの移動にもう1つ道(L1+L6+L4)が増えました。このようにあるところからあるところへ移動するのに道が1つしかなればその道を通ざるをえないが二つ道があったら交通の流れがどのように変化するか考えてみる。
点AからFまでのすべての点が各点へ移動するのに点BとEを結ぶ道の利用者を見るには、人が効率的なほうを選ぶとするなら、高いよりは安すく、時間がかかるよりは短時間な方を選ぶことになるので、まずL6を必ずとおるパターンと、とおらないで移動するパターンのうちもしL6をとおらないで移動するよりも、L6をとおるった方のが枝の長さが短かれば、L6をとおるだろう。(L6をとおる=L6をとおらない>L6をとおる)逆であればL6はとおらない道を選ぶだろう。つまりここでは枝(距離や時間、道路利用料金)としているものの長さが短いほうを選ぶだろう。
各出発地から各目的地にそれぞれ流れると考えられるパターン
| 入/出 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| A | - | L1 | L1+L2 | L1+L2+L3 | L1+L2+L3+L4 | L1+L2+L3+L4+L5 |
| A' | - | L1 | L1+L6+L4+L3 | L1+L6+L4 | L1+L6 | L1+L6+L5 |
| B | L1 | - | L2 | L2+L3 | L2+L3+L4 | L2+L3+L4+L5 |
| B' | L1 | - | L6+L4+L3 | L6+L4 | L6 | L6+L5 |
| C | L2+L1 | L2 | - | L3 | L3+L4 | L3+L4+L5 |
| C' | L3+L4+L6+L1 | L3+L4+L6 | - | L2+L6+L4 | L2+L6 | L2+L6+L5 |
| D | L3+L2+L1 | L3+L2 | L3 | - | L4 | L4+L5 |
| D' | L4+L6+L1 | L4+L6 | L3 | - | L3+L2+L6 | L3+2+L6+L5 |
| E | L4+L3+L2+L1 | L4+L3+L2 | L4+L3 | L4 | - | L5 |
| E' | L6+L1 | L6 | L6+L2 | L6+L2+L3 | - | L5 |
| F | L5+L4+L3+L2+L1 | L5+L4+L3+L2 | L5+L4+L3 | L5+L4 | L5 | - |
| F' | L5+L6+L1 | L5+L6 | L5+L6+L2 | L5+L6+L2+L3 | L5 | - |
結果
上記のパターンから
アクアラインを利用した場合(料金、時間等) < アクアラインを利用しない場合(料金、時間等)になるものを選ぶ。
結果6つのパターンの式が出た。
① L6 < L2-L4-L3
② L6 < L2+L3-L4
③ L6 < L2+L3+L4
④L6 < L3+L4-L2
⑤ L6 < L3-L4-L2
⑥ L6 < L4-L3-L2
さらにそれらを6つのパターン式から、計算を続けてみると、L2,L4,L6よりもL3が一番大きな数字であれば、L6を利用することがわかった。 つまり、6つの点がすべての点へ移動するのに点BとEを結ぶ道があったら、点CとDを結ぶ枝の長さL3が大きな数字であるほど(時間がかかるあるいは有料料金が高くなるほど)L6を利用する人が増えることになる。
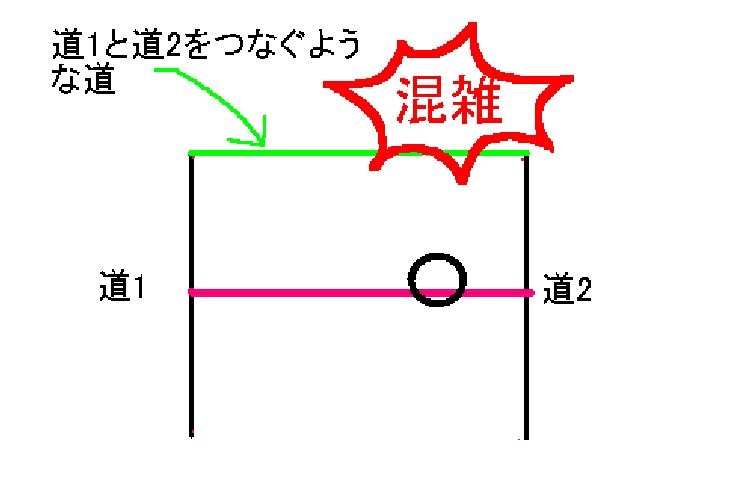 言い換えると、コの字型に道路ネットワークがあって、つなぎになるような道が混雑する場合それを解消する一番よい方法は、道路ネットワークをロの字型にするよりも両サイドにある道1、道2の中間を結ぶ道をつくると、道路ネットワークの全体の流れがよくなるということになる。
言い換えると、コの字型に道路ネットワークがあって、つなぎになるような道が混雑する場合それを解消する一番よい方法は、道路ネットワークをロの字型にするよりも両サイドにある道1、道2の中間を結ぶ道をつくると、道路ネットワークの全体の流れがよくなるということになる。
第四章 実際の数字代入
A=横須賀、B=浮島、C=湾岸市川、D=市原、E=木更津金田、F=富浦 間の料金、所用時間を L1=(横須賀、川崎浮島)、L2=(川崎浮島、湾岸市川)、L3= (湾岸市川、市原)、 L4=(市原、木更津金田)、L5= (木更津金田、富浦)、L6=(川崎浮島、木更津金田)と設定して6つのパターンのうち現実の距離と料金を代入して式が成り立つか計算してみる。
結果
| 入/出 | A | B | C | D | E | F | |
|---|---|---|---|---|---|---|---|
| A | - | 約1400円 約70分 | 約2400円 約100分 | 約3600円 約130分 | 約4600円 約140分 | 約7300円 約230分 | |
| A' | - | 約1400円 約70分 | 約7600円 約130分 | 約6400円 約100分 | 約5400円 約80分 | 約8100円 約170分 | |
| B | 約1400円 約70分 | - | 約1000円 約30分 | 約2200円 約60分 | 約3600円 約70分 | 約8100円 約170分 | |
| B' | 約1400円 約70分 | - | 約6200円 約70分 | 約5000円 約40分 | 約4000円 約15分 | 約6700円 約100分 | |
| C | 約2400円 約90分 | 約1000円 約30分 | - | 約1200円 約30分 | 約2200円 約50分 | 約4900円 約140分 | |
| C' | 約7600円 約140分 | 約6200円 約70分 | - | 約6000円 約60分 | 約5000円 約40分 | 約7700円 約130分 | |
| D | 約3600円 約120分 | 約2200円 約50分 | 約6000円 約60分 | - | 約1000円 約20分 | 約3700円 約100分 | |
| D' | 約6400円 約110分 | 約5000円 約40分 | 約6000円 約70分 | - | 約6200円 約70分 | 約8900円 約160分 | |
| E | 約4600円 約140分 | 約3600円 約70分 | 約2200円 約50分 | 約1000円 約20分 | - | 約2700円 約90分 | |
| E' | 約5400円 約90分 | 約4000円 約15分 | 約5000円 約40分 | 約6200円 約70分 | - | 約2700円 約90分 | |
| F | 約7300円 約230分 | 約6300円 約160分 | 約4900円 約130分 | 約3700円 約100分 | 約2700円 約90分 | - | |
| F' | 約8100円 約170分 | 約6700円 約100分 | 約7700円 約130分 | 約8900円 約160分 | 約2700円 約90分 | - |
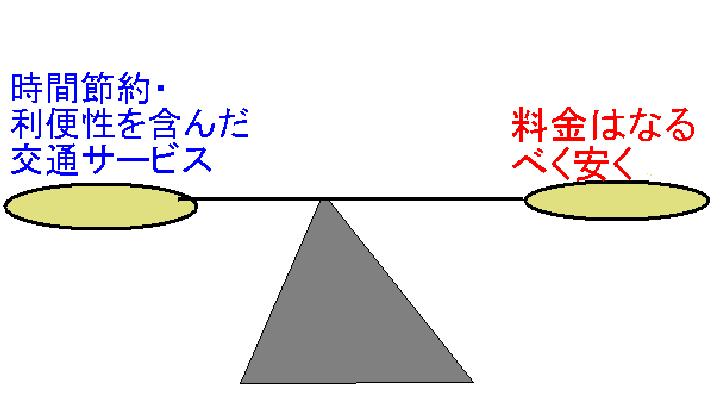
時間だけで考がえると単純モデルは成り立つが、道路利用料金だけで考えるとL6の枝が一番高いので単純モデルは成り立たない。つまり、ベイエリアの交通利用者は時間の面と料金の面を天秤に乗せどちらかに傾いているからアクアラインを利用する人と利用しない人が出てくることになる。
第五章 考察
①料 金・・・アクアラインを利用した場合にかかる道路料金
②料 金・・・アクアラインを利用しない場合にかかる道路料金
(①料金-短縮時間)<②料金・・・アクアラインを利用する
短縮時間・・・時間をお金の価値に換算すると一時間=750円(千葉)、830円(東京)、780円(横浜・川崎)※コンビニアルバイト昼間の時間給平均より
まずアクアラインを利用すると時間短縮になるエリア
表1
短縮時間をお金の単位にあわせ(①料金-短縮時間)< ②料金の結果
表2
この結果ではまだ短縮時間を考慮してもなおアクアラインを利用した経路の料金の方が、アクアラインを利用しない経路の料金よりも高い。最大で約4000円も高いところもある。
第六章 結論
実際にアクアラインを利用している台数は一日あたり約10000台から25000台ほどあります。たんに目的地までの経路として通るだけの道路といった感覚ではなくアクアラインを観光スポットととして利用する人もいるだろうし、渋滞からも逃れらから、約700円から4000円の間の料金を多く払ってもいいと思う価値観の人たちが実際一日当り10000から25000いることになります。今回は一時間の値段を750円から830円と設定しました。この数字自体が妥当ではないと思う人のほうが多いいかもしれない。もしそうであれば、アクアラインを利用する行為は約700円から4000円よりもぐっと下がった値段になり、さらに利用することで払った金額よりも時間短縮できたことと、利便性、etc・・・をやすく買い物した感じることになります。
 謝辞
謝辞
最後にこの研究に当たって、根本先生には大変お世話になりました。そして、明海大学の三浦先生にも参考となるアドバイスをいただいたり、資料を貸していただきとても助かりました。本当にありがとうございます。
参考文献
・東洋経済出版 「道路投資の社会経済評価」 道路投資評価研究会著
・国際地学協会 「首都圏道路地図」
・道路公団のホームページ http://www.japan-higtway.go.jp
・アクアラインのホームページ http://www.aqua-line.com