シミュレーション 1999年度秋学期期末試験問題

　

解答上の注意

問題1～問題3の3つの問題があります．解答用紙への記入はどのような順番でもかまいませんが，どの問題についての解答なのかは明記してください．
解答用紙には，必要かつ十分な解の導出過程も記述すること.
問題用紙の最後の1枚はメモ用の白紙です．問題用紙のホチキスははずしてもかまいません．
解答用紙は５枚綴じになっています．解答用紙のホチキスははずさないでください．裏面を使用してもかまいません．解答用紙が不足したら手を挙げて要求してください．

　

問題1

ある単位正方領域（一辺の長さが1の正方形）内に描かれた適当な図形領域の面積を求める一つの方法として以下のようなやり方が考えられる．

方法	Step1: 単位正方領域にN個の「でたらめに」点をばらまく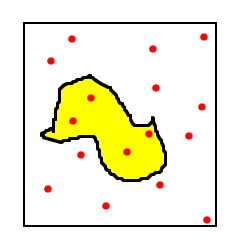．	図1：単位正方領域に描かれた適当な図とでたらめな点．
	Step2: 描かれた図形領域内に入っている点の数を数える．（a個だったとする）
	Step3: 単位正方領域内に描かれた図形領域の面積はa/Nと推測できる．
例題	右の図1は単位正方領域とそこに描かれた適当な図形領域を，そして，点はでたらめにばらまいた点を示す．ばらまかれた点は16個，描かれた図形領域内の点はそのうち4個である．よって，描かれた図形領域の面積は4/16=1/4と推測できる．

以下の問に答えよ．

（1）	上記の方法で描かれた図形の面積を推定する場合，より精度を挙げるにはどのような工夫が必要か．簡潔に述べなさい．
（2）	この方法を表計算ソフト用いて実現したい．正方単位領域内のでたらめな点はどのように発生させればよいか簡潔に説明しなさい．
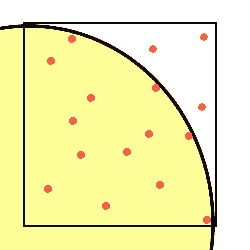
（3）	単位正方領域の左下隅の角を中心とした単位円（半径1の円）が正方領域上に描かれている（右図参照：単位正方領域上では1/4-円のみが関係する）．上記の方法で，1/4-円の面積を表計算ソフト（またはある言語）を用いて実験を通して推定したい．どのようにすれば1/4-円の面積を推定できるだろうか．具体的に実験方法を説明せよ．必要ならば以下のヒントを利用しても良い．ヒント: 円の中心が原点(0,0)の半径1の円の内部領域はx²+y²<=1の不等式で表現される．これを利用すると，例えば，(x,y)=(0.3,0.7)という座標で表現される点は(0.3)²+(0.7)²=0.58<1なので円領域内の点であることがわかる．一方，(x,y)=(0.9,0.8)という座標で表現される点は(0.9)²+(0.8)²=1.45>1なので1/4-円領域外の点であることがわかる．
（4）	上記の実験を利用して円周率πを求めたい．どのように応用すればよいのか簡潔に述べよ．ちなみに,一般的な円の面積はπr²である(rは円の半径を示す).

　

問題2

M/M/1/(∞)型の待ち行列系（到着率がλ，サービス率がμ）の解析を行いたい.以下の問に答えよ.

（1）	M/M/1/(∞)型の待ち行列系とは具体的にはどのような待ち行列系なのか．そのモデルの意味を簡潔に答えよ.
（2）	到着率λ,サービス率μとはどのような意味を持つ数字なのか.簡潔に説明せよ.
（3）	ある時刻t において系内に客がn人いる確率をP_n(t)とする. 時刻tに系内に客のいない確率P₀(t)と客が1人いる確率P₁(t)との間には P₁(t) = (λ/μ)P₀(t) の関係があるという.どのようにしてこの状態方程式が得られるのか概説せよ.導出の際に以下の事実は解説無しで利用してかまわない.
	解析の中で解説無しで利用してよい事実わずかな時間Δt 内に1人の客が到着する確率はλΔt わずかな時間Δt 内に1人の客のサービスが終了する確率はμΔt わずかな時間Δt 内で確率P_n(t)は変動しない. (Δt)²=0とみなしてよい.
（4）	確率P_n+1(t)と確率P_ｎ(t)と確率P_n-1(t)の間には P_n+1(t)-P_ｎ(t) = (λ/μ) {P_n(t)-P_ｎ-1(t)} の関係があるという.上記小問（3）の情報と併せて,確率P_ｎ(t)を導出せよ.

　

　

問題3

A君の利得表が次のように与えられている，A君とB君の2人ゲームがある．A君,B君それぞれの最適戦略を導出せよ.

A君の利得表		B君の選択肢
A君の利得表		X	Y
A君の選択肢	α	1	-4
A君の選択肢	β	-1	3

　

作成：	根本俊男
	(文教大学情報学部経営情報学科)
	e-mail: nemoto@shonan.bunkyo.ac.jp
実施：	1999年12月10日