米出荷時に起こる待ち行列の原因解明
文教大学 98p21056 河野恵介
1章 はじめに
北海道深川市は、お米の産地であり毎年9月の中旬から10月上旬までの約25日間米の出荷が行われる。農家の人は米を刈入れた後、その米を乾燥し農協へと出荷するのだが、その際地元の農家(全145世帯)のトラックがいっせいに集まるため農協には早朝6時頃から長蛇の待ち行列が起こる。米の出荷がピークの時期になると夕方5時ごろまで行列が絶えることは無い。待ち行列がやっと無くなったと思っても農協職員は米の処理が残っているため、終わるのが深夜の12時頃だ。それが毎日続き職員の顔にはもはや生気は感じられなかった。そこで私は農家や農協職員の疲労を少しでも減少するように何か無いかと考え、待ち行列が発生するのは出荷経路に原因があるのではないのかと思いその原因を解明することを考え、それによって少しでも出荷がスムーズに進行するようになればよいと思いこの課題に取り組むことにしました。


上図 深川市納内町全景
2章 問題点
米出荷時に起こる待ち行列の原因解明を考えるにあたって、現在の出荷のどの工程が1番ボトルネックになっているのだろうというのが問題になる。単純に考えればボトルネックになっている部分は農家に米の出荷において時間や量の制限がされていないという点である、それならば制限させるのが1番最適なのではという考えが浮かぶのだが、制限させるにも最適な制限を考えなければ意味が無い。有効な制限方法、または他の有効な原因解明がORを使ってできるのではないだろうか。
3章 現状
製品タンク 貯蔵タンク![]()
![]()
![]()
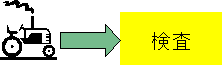
現在の米の出荷は対象農家全145世帯で、農家は米を刈入れ乾燥してから農協に出荷する。農協に持ってきてからは出荷経路としてまず米の痛み具合やランクを決めるため検査をする。検査が終わると次に重量を測り受け口(2つ)へ米を流す。流された米はいったん貯蔵タンクへ移され、コンテナへ入れるために一時製品タンクへ移されそしてコンテナへ移し製品として倉庫に保管さるという流れになっている。
貯蔵タンク コンテナ 倉庫

![]()
![]()
![]()
図 出荷経路
米は1年間(米の出荷時期は約25日である。)で約5万俵(3000㌧)の出荷がある。処理施設の処理能力は1日稼働時間が約8時間で1時間に約15000㎏(15㌧)・1日に約120000㎏(120㌧)である。しかしピーク時は1日約192000㎏(192㌧)を処理し1日の稼働時間は約13時間もの時間になる。
|
|
処理能力 |
|
1時間 |
15000㎏ |
|
1日(8時間) |
120000kg |
|
1年間(25日) |
3000000kg |
表 処理能力
現在の処理方法では農家のトラックはいったいどのくらいの待ち台数が発生しているかを待ち行列理論を用いて1500回シミュレーションしたところピーク時に70台の出荷があり平均最大系内数は23.7台、平均平均系内数は10.38088という結果が出た。(実験方法の詳細は次章にて説明)


図 出荷時の行列風景
4章 実験方法
今回、トラックの待ち台数の現状を調べるにあたって待ち行列理論を使用した。実験は平均到着間隔を平均到着率(単位時間内の到着数)をλと置き=1/λとする。サービス時間に関しても平均サービス率(単位時間内のサービス数)をμと置くと=1/μとなる。
今回の場合は、前章の現状データより平均到着率(λ)=7(人/時間)で、平均到着間隔(1/λ)≒0.142(時間)≒8.5(分)となり、サービス時間も同様に計算するとμ=5(人/時間)、1/μ=0.2(時間)=1.2(分)となった。
これらのデータをもとに乱数を発生させ“でたらめ”な到着・サービスをシミュレーションし平均最大系内数、平均平均系内数を調べた。なおここでの“でたらめ”の 定義は無記憶性(前の客と次の客との関連なし)・定常性(平均に客の到着・サービスは同じ)・希少性(同時に二人以上の客の到着・サービスは希)であることをいう。エクセル
5章 仮説
この章では2章でのボトルネックになっている部分というのを考え待ち行列が起こる原因の仮説をいくつか立てていき、それをもとに次章で検証していきたい。
仮説1
なぜ現在の処理方法では長蛇の待ち行列が発生するのだろうか。現在処理施設には受け口が2つあり、農家は量に関係なく到着した順に米の処理を行う。当然量の多い農家は受口においてかかる時間は長く、その間に多くの待ち行列が発生する。
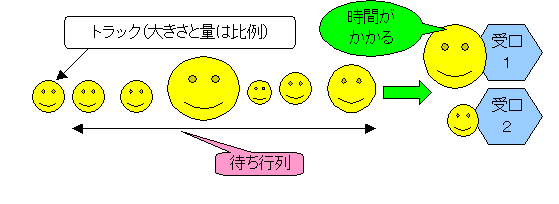
図 現状
そこで待ち行列が起こる原因として米の量が多いトラックがネックになっているのではないかと思い、米の量が多いトラックと少ないトラックを分けてそれぞれ受口1、受口2で処理すると待ち行列が減少するという仮説を考えた。
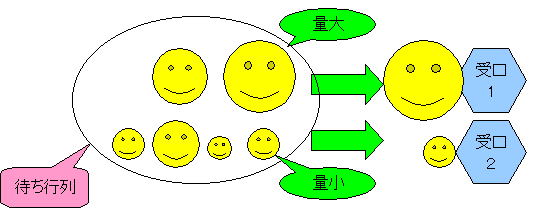
図 検証1
6章 検証
前章では待ち行列が発生する原因の仮説を立てたのだが、はたしてその仮説が原因となっているのだろうかということを検証するにあたって、待ち行列理論を使用したいと思う。ピーク時の一日の出荷台数、全出荷量、処理施設稼働時間から平均到着率(単位時間内の到着数、λ)、平均サービス率(単位時間内のサービス数、μ)を求め、これをもとに到着時間とサービス時間の値を出す。ちなみに到着時間とサービス時間は乱数を発生させて導き出している。ここでのサービス時間とは出荷する米を受け口に流し込んでいる時間である。
6-1 仮説1の検証
前章で米の量が多いトラックと少ないトラックに分けるとあったが検証では3000以上、以下で分けてみたところ3000以上のトラックが25台、3000以下のトラックが45台だった。待ち行列理論を使用して1500回以上シミュレーションした結果以下のようなデータが得られた。シミュレーションは4章の実験方法と同じでデータは以下の表より行った。
|
|
平均到着間隔1/λ(時間) |
平均到着率λ(人/時間) |
平均サービス間隔1/μ(時間) |
平均サービス率μ(人/時間) |
|
出荷量3000以下(受口1) |
0.22 |
4.5 |
0.26 |
3.75 |
|
出荷量3000以上(受口2) |
0.4 |
2.5 |
0.533 |
1.875 |
表 実験データ
表 現状
|
現状(受け口1・2) |
|
|
|
|
最大系内数合計 |
80637 |
平均系内数合計 |
17439.88 |
|
実験回数 |
3392 |
実験回数 |
1680 |
|
平均最大系内数 |
23.7727 |
平均平均系内数 |
10.38088 |
表 仮説1でのシミュレーション結果
|
出荷量3000以下(受け口1) |
|
|
|
|
実験回数 |
2629 |
平均系内数合計 |
8280.4 |
|
最大系内数合計 |
32509 |
実験回数 |
1671 |
|
平均最大系内数 |
12.36554 |
平均平均系内数 |
4.955356 |
|
出荷量3000以上(受け口2) |
|
|
|
|
実験回数 |
3570 |
平均系内数合計 |
6908.674 |
|
最大系内数合計 |
35783 |
実験回数 |
1664 |
|
平均最大系内数 |
10.02325 |
平均平均系内数 |
4.151847 |
このデータより現状は、平均最大系内数23.7727(台)・平均平均系内数10.38088(台)に対し仮説1では、平均最大系内数12.36554+10.02325=22.38879(台)・平均平均系内数4.955356+4.151847=9.107203という結果が得られた。
7章 結果
7-1仮説1の結果
前章で行った実験結果をみると現状では平均最大最大系内数23.7727(台)・平均平均系内数10.38088(台)、仮説1の受口をそれぞれ3000kg以下・3000kg以上に分けた方法では、平均最大系内数12.36554+10.02325=22.38879(台)・平均平均系内数4.955356+4.151847=9.107203という結果が得られ最大系内数が1.4台・平均系内数が1.2台でともに約1台少なくなるという結果がとなった。
8章 まとめ
6章で現在待ち行列が起こる原因は米を流す受口にあると仮説をたてそれを待ち行列理論を使用しシミュレーションした結果、最大系内数・平均系内数がともに約1台減少するということがわかった。この結果に関して、減少が約1台というのは少ないのではないかと思うのだが、全体で考えてみると最大系内数は現状より約5.8%の減、平均系内数にいたっては1割も減少した。6章のような簡単な仮説でもこれだけの成果があるということは、やはり米出荷時に起こる待ち行列の原因は米の受口にあるということがこの研究で解明された。
9章 おわりに
今回の研究では米出荷時に起こる待ち行列の減少の原因解明をしたが、今後この研究を続けていきさらに良い原因解明ができるように努めていきたいと思います。あと今回の研究で私自身待ち行列の難しさを知ることができ、そして待ち行列について少しでも詳しくなれたことに喜びを感じています。
謝辞
今回の卒業論文を作成する際に根本先生には大変お世話になりました。どうもありがとうございました。JAきたそらち納内支所の皆様、お忙しい中、資料の提供や取材などをさせていただきどうもありがとうございました。ゼミ生の皆さんいろいろなアドバイスありがとうございました。
参考文献
根本俊男、レジュメ(Queueing theoryⅠ待ち行列をシミュレーションする・Ⅱ待ち行列を解析する)、2000(http://www.bunkyo.ac.jp/nemoto/lecture/)
雨宮幸雄、待ち行列必勝作戦、1995、オーム社雑誌局
参考資料
JAきたそらち納内支所、米資料、1999