 問題1
問題1 問題1
問題1文教堂は様々なイベント企画を手がけている.今回あるプロジェクト(「プロジェクトB's」と名付けられている)を企画することとなり,稲葉さんがプロジェクトリーダーとなった.稲葉さんはまずはプロジェクトの全体を把握したいと考え,その作業リストの作成を若手社員の松本君に依頼した.後日,松本君から提出された作業リストは表1-1に示されたものである.
表1-1:プロジェクトB'sの作業リスト(作成者:松本)
| 作業名 | 所要日数 | 先行作業 |
| S | 7 | なし |
| R | 5 | なし |
| A | 8 | S, R |
| B | 7 | S, R |
| C | 4 | A, R |
| D | 6 | S, R |
| E | 5 | C, R |
| F | 24 | なし |
| G | 7 | A, B, R |
| H | 5 | A, B, C, D, R |
| I | 3 | E, H, R |
| J | 4 | F, I, R |
松本君から提出されたプロジェクトB'sの作業リストを見て,プロジェクトリーダーの稲葉さんと松本君が会話をしている.
稲葉:『プロジェクトの作業の洗い出しはうまくできているようだ.私も,この12個の作業で今回のプロジェクトは捉えられると思うよ.また,各作業の所要日数は,松本君の試算を信じることにしよう.ところで,先行作業は冗長な情報も書かれているようだけど.きちんと吟味した?』
松本:『先行作業に冗長な情報?それって何ですか?』
稲葉:『例えば,作業Cの先行作業に注目してごらん.作業Cの先行作業は作業Aと作業Rだけど,一方の作業Aの先行作業にも作業Rは含まれているだろ.そういうことは,作業Cの先行作業に作業Rが記入されていなくとも,作業Cの先行作業に作業Aが記入されているだけで,自動的に作業Rも作業Cの先行作業になっていることになるよね.だから,作業Cの先行作業に作業Rを記入するのは冗長な情報になるよね.』
松本:『確かに.でも,冗長な先行作業の情報を見つけるにはどうしたらよいのですか?』
稲葉:『ん〜.どうするんだろ?(痛いところを聞いてくるぞ.)でも,このぐらいの作業リストならどんな方法でも何とかなるんじゃないかな.ともかく,先行作業の冗長な情報が多く含まれているとアローダイアグラムを書いたりするときに面倒だからなるべく冗長な先行作業の情報は無いほうがいいよね.書き直してきて.』
以下の問いに答えよ.
| (1) | プロジェクトB'sにおいて,先行作業に冗長な情報がない作業リストを作成せよ. |
| (2) | プロジェクトB'sをアローダイアグラムで表現せよ.また,各イベントの最早イベント開始時刻,最遅イベント開始時刻も併記せよ. |
| (3) | 各作業のPERT計算表を作成せよ. |
| (4) | クリティカルパス上の作業をすべて列挙せよ. |
数日後,プロジェクトB'sの作業のいくつかは確定的な所要日数ではなく,ばらつきがあることが判明した.そこで,松本君は3点見積もり法を用いて新たにスケジュールを計画しなおすことにした.3点見積もり法の実施で必要なデータは以下の表1-2のようにまとめられた.必要があれば,別紙の正規分布表を利用せよ.
表1-2:プロジェクトB'sの作業とその所要日数に関するデータ(作成者:松本)
| 作業名 | 楽観値 |
最可能値 |
悲観値 |
作業日数のばらつき |
| S | 7 | 7 | 7 | 無し |
| R | 5 | 5 | 5 | 無し |
| A | 4 | 7 | 16 | 有り |
| B | 7 | 7 | 7 | 無し |
| C | 4 | 4 | 4 | 無し |
| D | 6 | 6 | 6 | 無し |
| E | 5 | 5 | 5 | 無し |
| F | 24 | 24 | 24 | 無し |
| G | 3 | 6 | 15 | 有り |
| H | 1 | 4 | 13 | 有り |
| I | 3 | 3 | 3 | 無し |
| J | 1 | 4 | 7 | 有り |
以下の問いに答えよ.
| (5) | 作業日数にばらつきがあることが判明した4つ作業の作業日数の期待値と分散を推定せよ. |
| (6) | 作業Gの作業日数が5日以上かかる確率を求めよ. |
| (7) | このプロジェクトのプロジェクト完了時刻の期待値と分散を推定せよ.また,その標準偏差を概算せよ. |
| (8) | プロジェクトの完了が34日以内に完了する確率を求めよ. |
 問題2
問題2あるプロジェクトは8つの作業から構成されている.各作業の先行関係をアローダイアグラムに表したものが図2-1である.また,各作業の必要な作業日数,追加費用を支払うことで短縮可能な作業日数,および,短縮に必要な1日あたりの追加費用は表2-1にまとめられている.ところで,表2-1の短縮可能日数とは,標準作業日数から短縮できる日数のことである.例えば,作業Aは標準5日から2日間短縮可能なので,最短3日で作業を終えることも可能となる.
|
|
|
図2-1:プロジェクトのアローダイアグラム(各作業日数の記入は省略) |
表2-1:プロジェクトの作業に関する情報
| 作業名 | 標準作業日数 | 短縮可能日数 | 短縮費用 |
| A | 5日 | 2日 | 2百万円/日 |
| B | 10日 | 0日 | - |
| C | 7日 | 3日 | 1百万円/日 |
| D | 11日 | 2日 | 3百万円/日 |
| E | 4日 | 2日 | 5百万円/日 |
| F | 10日 | 5日 | 4百万円/日 |
| G | 5日 | 3日 | 6百万円/日 |
| H | 13日 | 0日 | - |
以下の問いに答えよ.
|
(1)
|
標準作業日数でプロジェクトが実行される時,プロジェクト完了時刻を求めよ. |
| (2) | 標準作業日数でプロジェクトは実行されると仮定する.最遅作業開始時刻に各作業を開始し,休み無しで作業を行った場合のスケジュールをガントチャートで示せ. |
|
(3)
|
図2-1で示されたアローダイアグラムにはカットは何通り存在するか. |
|
(4)
|
各作業の作業日数が標準作業日数であるとき,最小カット(minimum cut)を構成するのはどのような作業群か.また,その最小カットの情報から,短縮すべき作業と,その作業の経済的な最大短縮可能日数を求めよ. |
|
(5)
|
プロジェクト完了時間を短縮するための最小追加費用とプロジェクト完了時刻の関係を示すグラフを作成せよ. |
 問題3
問題3以下の文を読み,次の問いに答えよ.
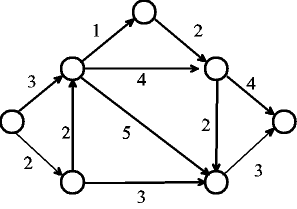
いくつかの点(○)の集まりと異なる2つの点を結ぶ枝(→)の集まりで描かれた図を有向グラフと呼ぶ.ある点から枝の向きに沿って次の点に移るということを繰り返したときにできる軌跡(移動経路にあたる点と矢線の系列)をパスと呼ぶ.
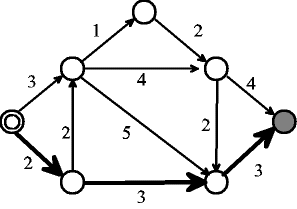
図3-1は有向グラフの例で,図3-2上の太線はその有向グラフ上での点◎から点●へのパスのひとつの例である.
有向グラフ上には一般的に複数本のパスが存在する.同じ点を繰り返し含むようなパスを閉路を含むと呼ぶ.閉路を含むパスが存在しない有向グラフを非閉路有向グラフと呼ぶ.図3-1は非閉路有向グラフの例でもある.
非閉路有向グラフには必ず入ってくる枝が存在しない点(開始点)と出て行く枝が存在しない点(終了点)少なくともひとつずつ存在する.また,トポロジカルオーダーで各点に順番を付けることが可能である.
|
(1)
|
図3-1で示された非閉路有向グラフを解答用紙に写し,各点にトポロジカルオーダーで順番をつけよ. |
| (2) | 図3-1で示された非有向グラフの例には開始点と終了点が各々いくつ存在するか. |
|
(3)
|
図3-1で示された非閉路有向グラフに開始点から終了点に至るパスは何通り存在するか. |
| (4) | 図3-1で示された非閉路有向グラフの各枝に付してある数字はその枝の長さを意味する.あるパスに対し,パス上の枝の長さの合計をそのパスの長さと約束する.図3-2において太線で示されたパスの長さを求めよ. |
| (5) | 図3-1で示された非閉路有向グラフに対して,開始点から終了点に至るパスの長さが最大であるパスを解答用紙に写したグラフ上で太線にし明示せよ.また,その長さを示せ. |
 |
 |
|||
|
図3-1:非閉路有向グラフ |
図3-2:パスの例(太線) |
| 作成: | 根本 俊男(文教大学情報学部経営情報学科) | 配点および講評 |  |
| e-mail: nemoto@shonan.bunkyo.ac.jp | |||
| 実施: | 2001年5月25日 |