うなぎ漁獲量の予測

95P21170

吉井 俊一


第１章：始めに


私は毎年１２月になると、うなぎ漁を始める。自分で漁業権を取得し、道具をそろえ、好きな時に取りに行くのが漁のスタイルである。取れるときは１日でけっこう儲かるのですが、取れない時は１日もうけゼロになる。完全歩合制の漁である。本研究ではこのうなぎ漁について考える。



１）うなぎ漁とは


うなぎ漁とはうなぎの稚魚である“シラスウナギ”をとる漁を指す。養殖のうなぎはこの“シラスウナギ”を育て成魚にしている。今日の技術では、うなぎの卵からシラスウナギにまで成長させることができないので、食べ物が分かっていないので。）うなぎの養殖はこのシラスウナギ漁にかかっているといえる。


２）動機


漁は、１２月から４月の期間のうち、とくに１２月下旬から１月下旬が中心。漁は水の中に入るわけではないが、毎日水辺（海辺）で座っているのはつらいし、効率が悪い。これを、「取れそうな状況の時だけ漁に行く。」というように効率よくしようと思いこの研究を始めた。


３）この論文の構成

２章では“うなぎの生体・漁”、

３章では“予測する手段・データ”、

４章では“回帰分析を行う”、

５章では“分析結果（1）”、

６章では“回帰式”、

７章では“原因とその対策”、

８章では“変数選択”、

９章では“分析結果（2）”、

１０章では“本研究で得られたこと”、

の順で論議を進める。

第２章：うなぎの生体・漁


１）うなぎの生体


河川で成長したうなぎは海に出て、遠い外海で産卵する。仔魚は透明で薄い柳のような形していて“レプトケファルス”と呼ばれる。これが変態して細長いしらすうなぎになる。しらすうなぎは夜行性で、昼間は砂に頭だけ出して寝ていて、河川に遡上するのは夜間に限られ、その際に潮の干満を利用する。日本産ウナギは河川に入ってきて１週間目位で体色が黒ずんでくる。日本では河口域で採補されたしらすうなぎは、養殖種苗として供給されるので、しらすうなぎの生態をしることは効率的な捕獲だけでなく合理的資源管理にも必要なことである。うなぎは昼間は砂に頭だけ出して寝ていて、夜に行動する、夜行性である。：参考文献[1]


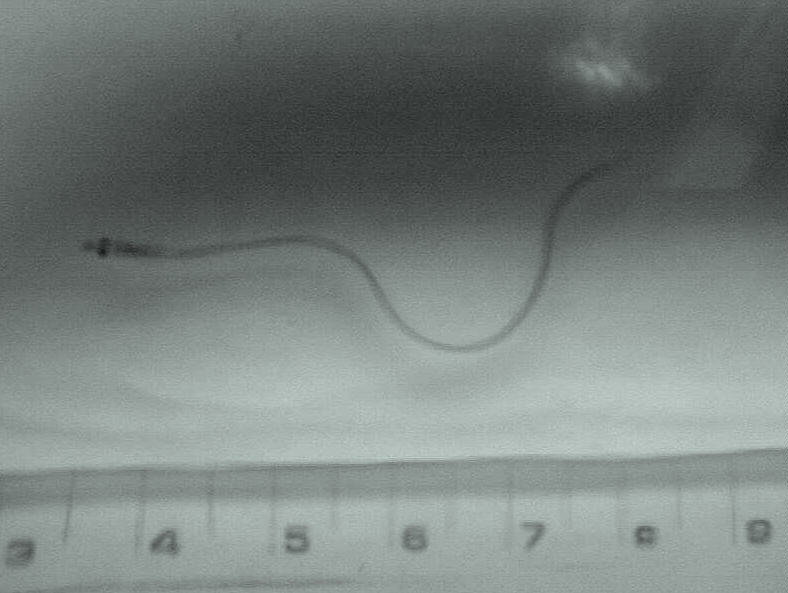
しらすうなぎ（体長約８ｃｍ）


２）うなぎ漁


ここではうなぎ漁について説明する。


・種苗用うなぎ稚魚「しらすうなぎ」採取


採取期間：１２月１日から翌年４月３０日まで。

採取区域

１：相模川河口の湘南大橋から下流と、平塚港。

２：花水川河口の花水橋から下流。


注意

・しらすうなぎは平塚漁業組合の許可を受けていないと取ることはできない。許可を受けないでうなぎを取ると６ヶ月以下の懲役または罰金刑になるので注意してほしい。


３）うなぎ漁の内容


日が暮れてから翌朝までの間で、干潮から満潮への過程が存在する日に行う。うなぎは夜間に満潮になるときの川を逆流する流れにのって川を遡上するので、海面に明かりをともし、その明かりで見える範囲を泳いだうなぎを網ですくってつかまえる。


　　　 相場は１ｇ（７、８匹）で４００円から９００円の間で上下する。取れている時は安く、取れない時ほど高くなる。

去年の１番良かった日は、１２月３０日（中潮）１時間半で９１ｇ（３６４００円）取れた。だいたい取れた日から３，４日は良く取れることが多い。結局この時は１週間で２８４ｇ（１２万円分ぐらい。）採れた。


論文の構成へ戻る。

　　　

第３章：漁獲量予測の手段


統計解析手法の中の“重回帰分析 ”を使用します。

１）データ


データは、うなぎの漁獲量（ｇ）、潮、漁に来ている人数、天気（雨・風）、気温、気圧（現地・海面）などを使用します。：[気象に関するデータ]


２）予備的解析とその必要性


使用するデータはグラフを活用して十分に吟味する必要がある。回帰分析などの多変量解析の手法は、外れ値の影響をうけやすく、又２つの変数の間の関係には直線関係を想定している事が多い。したがって予備的解析によって、外れ値の有無を検討したり、１つ、また２つの変数間の関係を検討することは極めて重要なプロセスになる。 （EXCELでは分析ツールの基本統計量を使うことによって、平均値や標準偏差などの基本的な統計量を算出できる。）


１変数ごとの解析

多変量データを構成する各変数ごとのデータの特徴を把握するために、１変数毎に基本統計量（平均値や標準偏差）の算出とグラフ表現を行なう。平均値と標準偏差の値がわかると、個々のデータが、外れ値かどうかを判断することができる。

平均値±2.5×標準偏差

の範囲を越えてるデータは、外れ値と考えられる。

データの分布や外れ値の存在は、データをグラフで表現し、視覚的に吟味することも必要である。この時用いるグラフとしては、ヒストグラム やドットプロットが有効である。


２変数ごとの解析

２つの量的変数があって、一方の変数データが変化したときに、もう一方の変数のデータもそれにともなって変化する場合、これら２つの間には相関関係があるという。相関関係の中でも、一方の変数の値が大きくなると、一方の変数の値も大きくなるという関係を正の相関関係といい、これとは逆に、一方の変数の値が大きくなると、もう一方の変数値は逆に小さくなるという相関関係を負の相関関係という。

相関関係の強さを測る指標が相関係数である。相関係数は、通常rという記号で表記される。相関係数は−１から＋１までの間の値をとり、相関係数の絶対値、あるいは相関係数の２乗値が１に近いほど相関関係が強いと判断する。相関係数の値が正のときには、正の相関関係があることを示唆していて、相関係数の値が負のときには、負の相関関係があることを示唆している。相関係数が０に近いときには、その２つの変数の間には、相関関係がないことになる。

２つの量的変数の関係も、１変数ごとの解析を行なうときと同様に、グラフで表現し、視覚的に吟味することが必要である。このためのグラフとして散布図がある。

散布図を視察する際のポイントは３つある。

１：変数の間にはどんな関係があるか（直線的か、曲線的か、無関係か）、

２：外れ値（異常に飛び離れた値）はないか、

３：いくつかのクラスター（グループ）が形成されてないか、である。


論文の構成へ戻る。

第４章：回帰分析を行なう

データを変数に置き換え、実際に回帰分析を行なう。


１）データを変数に置き換える。

データには量的なデータと質的なデータがある。量的なデータは数値で表してあり、質的なデータは数値以外で表してある。（大・中・小など。） 質的なデータを変数に変えるには、ダミー変数というものを使用する。


２）ダミー変数


ダミー変数とは０と１のどちらかの値しかとらない人工的変数である。例えば、性別のように２種類（男・女）ある時には、一方を１（男＝０・女＝１）と数値化する。血液型のように４種類（A,B,O,AB）ある時には、３つのダミー変数を使って、A：x1=1,x2=0,x3=0、B:x1=0,x2=1,x3=0、O:x1=0,x2=0,x3=1、 AB:x1=0,x2=0,x3=0とする。どれが基準となる血液型（上の例ではAB型）を決め、それを（０、０、０）とし、他の血液型は、どこか１つの値を０とする。基準は、解析者が任意に決める。

回帰分析を行なう。

各データの意味。（縦がサンプルで、横がデータです。）

＊潮 (ｃｍ)：潮の満ち引きの差。潮の種類はそれぞれその左に表示してある。

＊人数：漁に来た人の数。

＊風向（最多）：風向は質的データで、２種類だったのでダミー変数を使用。単位は（ｍ：メートル）です。

＊風（平均）：平均の風速。単位は（ｍ：メートル）。

＊気温（最高）：その日の最高気温。

＊気温（最低）：その日の最低気温。

＊気温（平均）：その日の平均気温。

＊降水量：その日の降水量。単位はｍｍ（ミリメートル）。

＊気圧（現地）：その日の現地気圧。−1000hPa（1000ヘクトパスカル差し引く）の形で表示。

＊気圧（海面）：その日の海面気圧。−1000hPa（1000ヘクトパスカル差し引く）の形で表示。

＊うなぎ：その日のうなぎの魚獲量。単位はｇ（グラム）。

    潮 (ｃｍ) 人数 風向（最多） 風(平均) 気温(最高) 気温(最低) 気温(平均) 降水量 気圧（現地） 気圧（海面） ウナギ
1 長潮 75 12 0 4.5 9.5 4.1 6.3 0 17.7 22.8 21
2 若潮 90 7 0 3.3 9.5 2.7 5.6 0 23 28.3 9
3 中潮 115 12 0 3.5 9.9 2.4 6.9 0 22.9 28.2 0
4 中潮 135 12 0 2.7 13.3 5.9 9.3 0 14.9 20 91
5 大潮 145 17 1 3.2 14.7 4.5 9.2 0 14.1 19.2 34
6 大潮 150 7 1 3 10.9 6.5 8 0 18.6 23.7 4
7 大潮 145 12 1 3.6 6.9 4.2 5.5 14 6.1 11.2 34
8 中潮 130 12 1 3 12.3 4.3 8.2 0 8.1 13.2 60
9 中潮 115 12 0 4 15 2.1 8.4 0 9.9 15.1 45
10 中潮 90 7 0 2.6 11.3 5.1 8.5 0 13.3 18.4 16
11 小潮 60 7 0 2.2 12.8 3.3 8.3 0 14.9 20 4
12 小潮 50 7 1 3.8 14.5 5.3 9.6 1 3.3 8.5 1

外れ値の有無を見る。

１：視覚的に見る・１変数ごとに外れ値の有無をみる。

各データの散布図をつくる。

グラフ１：潮 (ｃｍ)の散布図。

グラフ２：人数の散布図。

グラフ３：風向（最多）の散布図。

グラフ４：風（平均）の散布図。

グラフ５：気温（最高）の散布図。

グラフ６：気温（最低）の散布図。

グラフ７：降水量の散布図。

グラフ８：気圧（現地）の散布図。

グラフ９：気圧（現地）の散布図。

グラフ１０：気圧（海面）の散布図。


２：２変数ごとの相関をみる。

相関行列をつくる。



３：各データごとの残差グラフの作成。

各データの残差グラフをつくる。

グラフ１：潮 (ｃｍ)の図残差グラフ。

グラフ２：人数の残差グラフ。

グラフ３：風向（最多）の残差グラフ。

グラフ４：風（平均）の残差グラフ。

グラフ５：気温（最高）の残差グラフ。

グラフ６：気温（最低）の残差グラフ。

グラフ７：降水量の残差グラフ。

グラフ８：気圧（現地）の残差グラフ。

グラフ９：気圧（現地）の残差グラフ。

グラフ１０：気圧（海面）の残差グラフ。

何の傾向がない事が望ましい。何らかの傾向があるときには、モデルの不適合や、外れ値の存在が疑われる。



４:各データごとの観測値グラフの作成。

各データの観測値グラフをつくる。

グラフ１：潮 (ｃｍ)の観測値グラフ。

グラフ２：人数の観測値グラフ。

グラフ３：風向（最多）の観測値グラフ。

グラフ４：風（平均）の観測値グラフ。

グラフ５：気温（最高）の観測値グラフ。

グラフ６：気温（最低）の観測値グラフ。

グラフ７：降水量の観測値グラフ。

グラフ８：気圧（現地）の観測値グラフ。

グラフ９：気圧（現地）の観測値グラフ。

グラフ１０：気圧（海面）の観測値グラフ。

予測値の点よりも上にある点と、下にある点の数が、ほぼ同数であることが望ましい実測点の各点が予測値の点に近いほど、回帰式のあてはめがうまくいってることになる。


論文の構成へ戻る。


第５章：分析結果（1）

分析結果の検討や問題の有無をみる。



回帰統計
重相関 R 0.974454
重決定 R2 0.94956
補正 R2 0.445158
標準誤差 20.76556
観測数 12


分散分析表          
  自由度 変動 分散 分散比 有意 F
回帰 10 8117.708 811.7708 1.882548 0.517175
残差 1 431.2085 431.2085    
合計 11 8548.917      


  係数 標準誤差 t P-値 下限 95% 上限 95% 下限 95.0% 上限 95.0%
切片 -655.462 724.2367 -0.90504 0.531708 -9857.72 8546.798 -9857.72 8546.798
潮 (ｃｍ) 0.408452 0.317034 1.288355 0.4202 -3.61983 4.436733 -3.61983 4.436733
人 7.574973 3.953747 1.915897 0.306247 -42.6619 57.81188 -42.6619 57.81188
風向（最多） -57.6937 20.55493 -2.80681 0.217887 -318.868 203.4803 -318.868 203.4803
風(平均) -30.4516 18.54138 -1.64236 0.348183 -266.041 205.138 -266.041 205.138
気温(最高) 12.28777 10.95583 1.121573 0.463559 -126.919 151.4943 -126.919 151.4943
気温(最低) 26.86853 13.43588 1.99976 0.295198 -143.85 197.5868 -143.85 197.5868
気温(平均) -43.3404 24.13393 -1.79583 0.323456 -349.99 263.3089 -349.99 263.3089
降水量 -5.09646 4.125186 -1.23545 0.433194 -57.5117 47.31878 -57.5117 47.31878
気圧（現地） -176.162 151.1473 -1.1655 0.45144 -2096.66 1744.338 -2096.66 1744.338
気圧（海面） 169.0564 149.6187 1.129915 0.461217 -1732.02 2070.135 -1732.02 2070.135


残差出力      
観測値 予測値: ウナギ 残差 標準残差
1 19.3074 1.692597 0.270337
2 12.97494 -3.97494 -0.63487
3 -3.80665 3.806653 0.607989
4 83.55877 7.441229 1.188495
5 42.20415 -8.20415 -1.31035
6 1.663656 2.336344 0.373155
7 34.09773 -0.09773 -0.01561
8 55.40274 4.59726 0.734263
9 46.03171 -1.03171 -0.16478
10 30.31971 -14.3197 -2.28711
11 -2.38588 6.385876 1.019937
12 -0.36828 1.368279 0.218538

分散分析表の中の「有意Ｆ」の数値をみる。

有意Ｆの数値＜有意水準αならばＨ0を破棄する。（回帰式には意味がある。）

有意Ｆの数値＞有意水準αならばＨ0を破棄せず。（回帰式には意味がない。）

有意水準は、一般的には0.05に設定される。

有意Ｆの数値＝0.438457>0.05で（回帰式には意味がない。）



回帰式の有効性

回帰式の有効性を評価するには、寄与率（＝決定係数）を計算する。寄与率は目的変数ｙの変動のうちで、ｘをつかった回帰式によって説明のつく変動の割合を示す指標で、

寄与率＝回帰変動/合計の変動

でもとめられる。寄与率は１に近いほど回帰式のあてはめがうまくいってることになる。寄与率はＲ2という記号で表記される。

Ｒ2＝0.97333


論文の構成へ戻る。

第６章：回帰式

回帰式はｙ=-655.462+0.408452x1+7.574973x2-57.6937x3-30.45146x4+12.28777x5+26.86853x6-43.3404x7-5.09646x8-176.162x9+169.0564x10になる。しかし、”回帰式には意味がない”とでてきている。それはなぜなのか


論文の構成へ戻る。

第７章：原因とその対策


有効な回帰式にならない原因として考えられる事。

・有効でない変数が入ってしまっている。

・サンプル数が足りない。

の２つが考えられる。

対策として、

有効でない変数を探して、取り除く。



論文の構成へ戻る。

第８章：変数選択

説明変数が目的変数ｙの予測（説明）に役立つかどうかは、Ｆ値と呼ばれる統計量を利用する。

Ｆ値の求め方。

Ｆ={(偏回帰係数)/(偏回帰係数の標準誤差)}2

（例：潮：{(0.408452)/(0.317034)}2=1.659869685)

Ｆ値が２以上ならば有効な変数、２未満ならば不要な変数

として変数の選択を行なうと、良い回帰式が得られる。

選択した有効な変数は、

・人

・風向き（最多）

・風（平均）

・気温（最高）

・気温（最低）

・気温（平均）

の６個の変数である。これらをまた回帰分析していく。


論文の構成へ戻る。

第９章：分析結果（2）


回帰式ｙ=-24.97628856+6.11379515x1-18.51421564x2-12.05400151x3+9.010099732x4+13.86191008x5-16.38973016x6

有意Ｆの数値＝0.524321404>0.05で（回帰式には意味がない。）

という様な結果が得られました。

しかし、また“有意Ｆの数値”が0.05以下にならず、回帰式が有効でない。

原因

不要な変数は取り除いたので、サンプル数が足りないと考えられる。


論文の構成へ戻る。

第１０章：本研究で得られたこと

・有効な回帰式は得られなかった。（サンプル不足のため。）

・１番有効な説明変数は“人”と分かった。（相関行列上で。）

“人”の変数の中には、ただ単に、“人数のデータ”だけではなくて、“漁に関する人の経験”も、含んでしまっていると考えています。

今後、もっとサンプルをそろえ、“人の経験”を数値で表わせるようにしたうえで、回帰式をだせる様にしていきたいです。


参考文献

[1]川村軍蔵：魚類の生態から見た漁法の検討-４３、シラスウナギ（上）-生態、水産の研究、Vol.10,NO.6,PAGE.37-43,1991

[2]内田治：すぐわかるEXCELによる多変量解析

[気象に関するデータ]:横浜地方気象台にて複写
論文の構成へ戻る。 卒業研究に戻る