| 作成: | 根本 俊男 |
| (文教大学情報学部経営情報学科) | |
| e-mail: nemoto@shonan.bunkyo.ac.jp | |
| 実施: | 1999年7月9日 |
文教データ通信は2つの地上局と4つの人工衛星を用いてオーストラリアから東京への衛星通信事業を行なっている(表1を参照).各地上局・各人工衛星には送信用のアンテナと受信用のアンテナがあり,送信用アンテナからデータを送信し,受信アンテナがデータを受信することによりデータ通信を行なっている.
送信アンテナは技術的な理由で送信先をひとつの地上局または人工衛星に固定しておかなくてはならない.また,アンテナの性能と送信先の関係から各アンテナ毎に単位時間内に送信できるデータ量の上限(データ送信能力)がわかっている.さらに,データを送信する際は電力を消費するが,各アンテナごとに1Gbのデータ量を送るのに消費する電力量も計測されている.各送信アンテナのデータは以下の表1にまとめられている.
表1:文教データ通信の持つ通信網のデータ
|
地上局・人工衛星名
|
送信アンテナ名
|
固定送信先
|
データ送信能力 単位時間内に送信できるデータ量の上限 (データ量の単位:Gb) |
1Gのデータ量を送信するのに必要な電力量 (単位:Kw) |
|
オーストラリア地上局
|
オージー1号
|
人工衛星「春空」
|
30
|
2
|
|
オージー2号
|
人工衛星「夏空」
|
90
|
7
|
|
|
人工衛星「春空」 |
春1号
|
人工衛星「夏空」
|
60
|
8
|
|
春2号
|
人工衛星「秋空」
|
50
|
4
|
|
|
人工衛星「夏空」
|
夏1号
|
人工衛星「冬空」
|
40
|
3
|
|
夏2号
|
人工衛星「秋空」
|
20
|
6
|
|
|
人工衛星「秋空」
|
秋1号
|
日本地上局
|
60
|
7
|
|
秋2号
|
人工衛星「冬空」
|
60
|
2
|
|
|
人工衛星「冬空」
|
冬1号
|
日本地上局
|
30
|
4
|
|
冬2号
|
オーストラリア地上局
|
70
|
3
|
|
|
日本地上局
|
サムライ1号
|
人工衛星「春空」
|
80
|
2
|
|
サムライ2号
|
人工衛星「冬空」
|
0(故障中)
|
3
|
一方,受信アンテナは複数のアンテナから送信されたデータを同時に受け取ることが可能である. ある地上局または人工衛星の受信アンテナが複数の送信アンテナから同時にデータを受け取った場合は,受信した地上局または人工衛星の各送信アンテナから受信した合計データ量を適当に振り分けて送信することが可能である
また,各人工衛星にはデータを溜めておく機能がないので,受信したデータは必ず瞬時にすべて送信しなくてはならない.
以下の問いに答えよ.
| (1) | 文教データ通信の持つ通信網をネットワークで表現しなさい. |
|
(2)
|
上記小問(1)で表現に用いたネットワークのグラフ構造を隣接行列,接続行列,リストのそれぞれで表現しなさい. |
|
(3)
|
オーストラリア地上局から日本地上局へのデータ通信を行なう際の最大データ送信能力を算出しなさい. |
| オーストラリア地上局といくつかの人工衛星からなるグループ(日本地上局はいつでもグループに含まれないことに注意)からグループの外に送信できるアンテナのデータ送信能力の合計を「グループ送信能力」と呼ぶことにする. | |
| (4) | オーストラリア地上局と人工衛星「春空」からなるグループのグループ送信能力を算出せよ. |
| (5) | 文教データ通信の持つ通信網で最も小さいグループ送信能力を算出しなさい.また,最も小さいグループ送信能力を持つグループをすべて挙げなさい. |
| データをオーストラリア地上局から日本地上局へ送る際に消費される各送信アンテナの電力量の合計を送信消費電力と呼ぶことにする. | |
| (6) | オーストラリア地上局から日本地上局へ1Gbのデータを送信したい.送信消費電力が最も少ないの送信ルートを導け.また,導出したルートに沿って送信した場合の送信消費電力も算出せよ. |
| (7) | オーストラリア地上局から日本地上局へ40Gbのデータを送信したい.送信消費電力が最も少ないの送信ルートを導け.また,導出したルートに沿って送信した場合の送信消費電力も算出せよ. |
| (8) | オーストラリア地上局から日本地上局へ60Gbのデータを,日本地上局からオーストラリア地上局へ60Gbのデータを同時に送信したい.実現可能かどうか検討しなさい.実現可能な場合は,具体的な通信ルートを示し,実現不可能な場合はその理由を示せ. |
以下の問に答えよ.
| (1) | 最小木問題とはどのような問題か.定義を述べよ. |
|
(2)
|
最小木問題の知識を有効に利用することができる応用例をひとつ挙げよ. |
以下の問に答えよ.
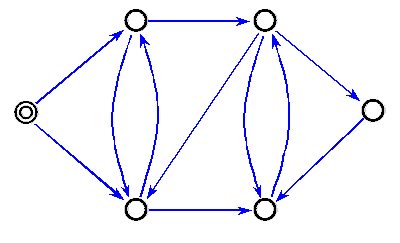
| (1) | 図1に示した有向グラフにおいて,二重丸の点(◎)から奥優先探索を行なった場合の探索木を図示せよ. |
|
(2)
|
図1に示した有向グラフの各点に後行順で番号付けをせよ. |

図1:有向グラフ